
A mechanical design can have an unlimited number of degrees of freedom, but if we are talking about gyroscope types, the number of degrees of freedom in a mechanical holonomic system can be no more than 6. Three directions of rotation around the axes are three degrees of freedom, and three along each axis are another three degrees of freedom, for a total of 6 degrees of freedom. Thus, permuting the axes in a system with coherent oscillations allows Gyro_6DoF to use the full 6 degrees of freedom, including both rotations and translational displacements. This makes the device unique, as it is able to compensate for and overcome gravity.
This idea works if Mach’s principle is confirmed. The inertial mass interacts with the long-range masses, and therefore its controlled distribution relative to the center of mass of the Gyro_6DoF rotor leads us to the holographic inertial forces. The necessary long-range interaction arises. This statement is relatively easy to verify in the experiment. The design of Gyro_6DoF suspended on torsion weights does not depend on the daily rotation of the Earth, and the balance of the torsion weights depends on the position relative to distant stars.
This article (first publication 5 Jan 2012)
https://web.archive.org/web/20120701000000*/www.isan.com.ua

describes a fundamentally new type of power astatic gyroscope — an unusual gyroscope with six degrees of freedom, which is described in my patent application with priority from 30.07.2013: http://www1.fips.ru/Archive/PAT/2015FULL/2015.02.10/DOC/RUNWA/000/002/013/135/971/DOCUMENT.PDF
Modular Generator of Gravitational Forces — A fundamentally new type of mechanical gyroscope with six degrees of freedom that needs urgent prototyping.
https://www.facebook.com/groups/Unusualgyro/?epa=SEARCH_BOX
Inventor: Alex Isakov
=================================================================================================
========================================================================
Leonard Susskind said, “The 3D world of ordinary experience—the universe filled with galaxies, stars, planets, houses, boulders, and people—is a hologram, an image of reality projected onto distant two-dimensional (2D) surfaces.” [39]. This seems strange to many, and understandably so since we have survived (through evolution) as clustered information on two halves of the same holographic horizon, processing bits of information like a hologram. This is super-efficient, but one time coordinate and one spatial coordinate in its purest form is an illusion, leading to numerous paradoxes and, ultimately, to a crisis in physics. It must be admitted that we have described a three-dimensional explosive mixture of illusion and reality in a deep study of the foundations of science. These seemingly speculative claims can be proven. It is necessary to build and study in detail a small device — the third and last of the possible types of power mechanical gyroscopes — a gyroscope with six degrees of freedom, previously unknown to science. As it turned out, it has holographic properties.
The theorem about the complete rotation of a physical body:
“To ensure complete rotation of a physical body around three axes in one cycle, a necessary and sufficient condition is the creation of angular displacements of its points in the main planes according to the laws of sine and/or cosine with a constant frequency and phase difference.»
====================================================================
Scientific hypothesis
==============================
Spherical motion of a rigid body is a motion in which:
Fixed point: One point of the body (the center of spherical motion) remains motionless.
Concentric spheres: The remaining points of the body move along trajectories lying on the surfaces of concentric spheres whose center coincides with the fixed point.
Freedom of rotation: The body can rotate around any direction passing through the fixed point, which makes the motion maximally free within the spherical coordinate system.
If add the dynamic condition that the angular motion of the body is described by harmonic laws (e.g. sine and/or cosine) with equal amplitude and frequency around all axes. In that case, this is a complete spherical motion.
Full spherical motion is the motion of a physical body in which the angular velocity is distributed over three axes forming an orthogonal coordinate system, with the following conditions being synchronously met:
Angular displacement: The angles of rotation of the body in each of the three main planes (XY, YZ, ZX) change according to a harmonic law (sinusoidally or cosinely) with the same frequency.
Phase synchronization: There is a constant phase difference between the angular displacements in each of the three planes, which determines the spatial orientation of the body at each moment in time.
Uniformity of amplitudes: The amplitudes of the angular displacements in each plane are equal and the maximum possible.
Uniform distribution of velocity: At each moment in time, the resulting three-dimensional angular velocity is a vector uniformly distributed over the sphere in space, ensuring the absence of preferred directions of motion.
This movement is unique because it creates a uniform effect in all directions in space and can be used to create new types of mechanical devices, such as Gyro_6DoF.
Full spherical motion is the motion of a physical body in which the angular velocity is distributed over three axes forming an orthogonal coordinate system, with the following conditions being synchronously met:
Angular displacement: The angles of rotation of the body in each of the three main planes (XY, YZ, ZX) change according to a harmonic law (sinusoidally or cosinely) with the same frequency.
Phase synchronization: There is a constant phase difference between the angular displacements in each of the three planes, which determines the spatial orientation of the body at each moment in time.
Uniformity of amplitudes: The amplitudes of the angular displacements in each plane are equal and the maximum possible.
Uniform distribution of velocity: At each moment in time, the resulting three-dimensional angular velocity is a vector uniformly distributed over the sphere in space, ensuring the absence of preferred directions of motion.
This movement is unique because it creates a uniform effect in all directions in space and can be used to create new types of mechanical devices, such as Gyro_6DoF.
«A complete revolution of a physical body is such a movement of the body around a fixed axis, during which each point of the body describes a complete circle around this axis.» If the rotation of the body occurs around one axis, it cannot be complete, since the number of independent coordinates is -3! A complete revolution of a physical body is a movement of the body around three axes in such a cycle, during which each point of the body describes a complete circle around each axis. A complete revolution of a physical body is a spherical motion of the body around three orthogonal axes (usually designated as the X, Y, and Z axes) in such a way that each point of the body describes a complete circle around each of these axes per cycle. This means that for a complete description of spherical motion, three independent angles (usually Euler angles) or three components of angular velocity are required. Now the most interesting part. Such a complete spherical motion of a physical body can be obtained only in the case (necessary and sufficient condition) if we produce angular displacements of its points in each of the main planes per cycle according to the laws of +/- sine and/or +/- cosine with a constant frequency and phase difference (we have the condition of coherent oscillations).
θx(t) = cos(θ)
θy(t) = sin(θ)
θz(t) = -sin(θ).
Where the angles are: θx — roll; θy — pitch; θz — yaw. Parameters θ = πt and -1 ≤ t ≤ 1; where θ is a geometric angle measured from an arbitrary direction clockwise from the corresponding major semi-axis, and t specifies the required accuracy of angular rotations. The formula of motion is specified parametrically and is applicable to any radius of spherical motion of a physical body. Additionally, we can determine the maximum possible number of directions of coherent oscillations, it is equal to 3^4 = 64. According to the definition of coherent oscillations, all elements of the mass of a physical body move along the surface of concentric spheres, around one fixed point. If we compare all points of a physical body with elements of its mass, we can conclude that we are dealing with a cooperative quantum phenomenon associated with accelerations. The number of possible pole trajectories is associated with the number of rotational accelerations of the elements of mass, which in turn are associated with fixed Cartesian coordinates.
For example, if the point intersects with the axis
x, the equation for angular displacement can be written as follows:
is the angular displacement in time.
This leaves one equation for each axis describing the angular displacement along that axis without the need to consider other axes or coordinates. This simplifies the problem to a minimum, keeping only the necessary rotation information.
======================================================================================
==================================================================================================
6 DoF

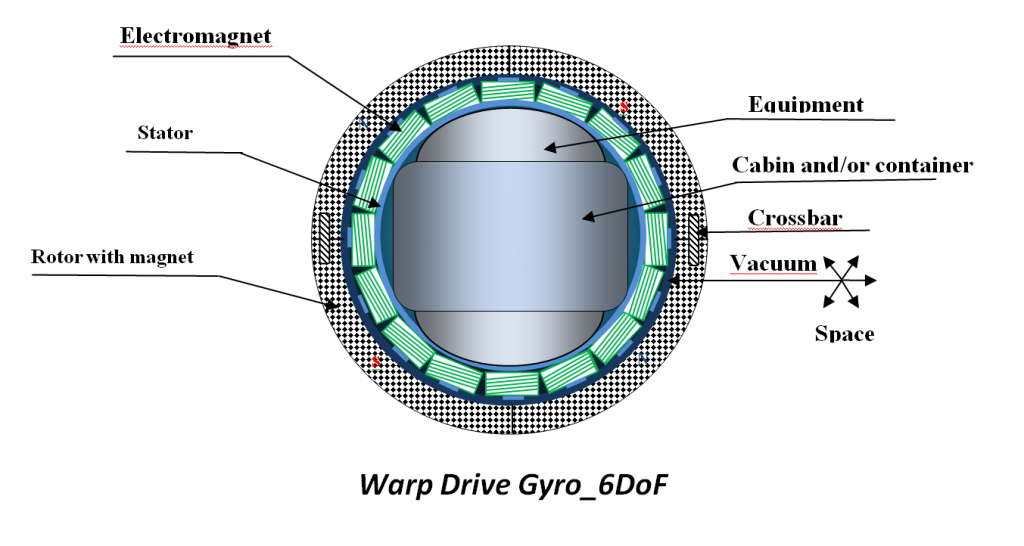
====================================================================================================================================================================================================================
Remote resonance virus killing



………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
The loud practical applications of an unusual gyroscope are a natural process, because, before us, holographic technology is a breakthrough in science.
Teleportation of physical objects
The teleportation phenomenon is based on the Нolographic Principle. Teleportation of physical objects is an unimaginable number of atoms that are interconnected and form a huge array of information data being moved. The very possibility of teleportation, not being limited by the distance and the speed of light, automatically appears in the device — a fundamentally new type of mechanical gyroscope with six degrees of freedom.
Teleporting physical objects without using exotic masses, energies, warp breaks and without losing information (as in the Star Trek series) can become closer to reality if the teleportation is based on the Holographic Principle. The concept of teleportation was originally developed during the Golden Age of 20th Century Science Fiction by authors who need the form of instant disembodied transport technology to support stories such as stories, example, The Fly (1958), The Return of the Fly (1959), The Curse of the Fly (1965) , The Fly (a remake of 1986) and The Fly II (1989).
The possibility of the existence of white holes was first proposed by the theoretical astrophysicist Igor Novikov in 1964. A white hole is a hypothetical region in space-time and a potential solution to the laws of general relativity, from which it follows that if black holes exist, then white holes must also exist in the universe. A white hole is the antipode of a black hole. Interestingly, a black hole has a huge mass, a white hole can be small at the level of apples. A black hole has tremendous energy, a white hole does not need such volumes since it draws energy from the energy of the physical vacuum. A black hole absorbs matter and a white hole repels, which is very important for its use as a natural insulating mechanism for a thermodynamic system. The Bekenstein-Hawking entropy should be equally applicable to both white and black holes since the definition of Boltzmann’s entropy does not depend on the direction of time. A black hole has maximum entropy — the entropy of a white hole decreases and tends to zero. When analyzing the characteristics of black holes, arising from the theory, it was noted that a black hole must rotate very quickly around one axis. And if the entropy of an object decreases, then the white hole must rotate around three axes per cycle, which is confirmed by computer simulations. Diametrically opposite differences can be enumerated for a long time. It is necessary to look at the problem from this position, and it will become clear that today there are no technical problems for creating a small artificial white hole at the level of «apples» and on the basis of a fundamentally new type of mechanical gyroscope with six degrees of freedom, the rotor of which rotates around three axes for the cycle — GYRO 6DoF. Inside the rotor of the GYRO 6DoF, there is a stationary container for teleporting physical objects, and such a white hole can move without restrictions on distance and speed of light under the control of a computer system. There is no need to disassemble the object into elementary particles and collect it somewhere else. The artificial white hole as a teleport is a new type of mechanical gyroscope with six degrees of freedom that does not violate the fundamental laws of physics.
Today, the teleportation of physical objects can become a reality, and the surprising fact is that at the same time, in one fairly simple device, harmoniously combining and automatically solved many problems of modern physics. This is a fundamentally new type of astatic gyroscope (an unusual gyroscope) — a device. The essence of the teleportation idea is that a spherical (thick-walled) solid-state, specially oscillating rotor should be inside in a vacuum in the external stator and inside itself (in the evacuated cavity) contain internal stationary stator, as well as a cabin or container for teleported physical objects.
The design is launched into deep space to isolate the thermodynamic system and freed from the external stator, and the rotor continues to produce high-speed three-dimensional rotation under computer control, as in slow motion from a simulator using the coherent oscillation formula. Coherent oscillations everybody points of the rotor leading to the appearance of a stationary interference pattern from the accelerations of the elements of its mass. By analogy with the concept of coherent radiation, the concept of coherent substance means that all the microscopic elements that make up a macroscopic rotor are in exactly the same state, including characterized by wave functions with a constant phase difference. The coherent state of a solid substance — particles of a massive rotor — isolates the particles (evacuated internal stator and container) from the quantum entanglement of their projections with the projections of particles of the external environment.
Full forced rotation of a spherical rotor with magnets is carried out around the spherical surface of the stator with inductors in a vacuum and around three fixed axes of Cartesian coordinates per cycle. Energy is spent only on maintaining the rotation of the rotor around one axis, around the remaining two axes the rotor rotates itself and causes a double-free emf in the stator coils (the spacetime vacuum provides a solution that also satisfies the definition of the teleportation, concept is based on the now-accepted fact that the vacuum is characterized by physical parameters and structure that constitutes an energetic medium and that pervades the entire extent of the Universe). Obtained in double recovery mode in an unusual gyroscope, the inexhaustible free energy of a vacuum allows for controlled oscillations of the rotor and its jerks (jerk is the first derivative of acceleration), we have all 64 possible options for teleporting physical objects as projected without loss onto the holographic screen (horizon) of the Universe of information … .
Today, the camp of theoretical physicists is divided, some believe that the degrees of freedom of the world consist of fields filling the Universe, others believe that the immediate use of Occam’s razor in three-dimensional space is required to understand the meaning of quantum gravity and apply it for practical purposes. In other words, they claim that two coordinates plus a single time coordinate are real, and one of the three coordinates is an illusion. The evolution of information processing (with losses) has led us to see the world as three-dimensional. According to the holographic idea, the world is about as rich in structure as the two-dimensional discrete lattice theory with an interval of the order of the Planck length. However, in reality, instead of a three-dimensional lattice, a full description of nature requires a two-dimensional lattice on two halves of a spherical surface along which projections of elementary particles move in pairs and this is enough to describe the spatial boundary of the world. In a certain physical sense, the world is two-dimensional, not three-dimensional, as previously assumed.
Holographic performance dates back to Gerard ‘t Hooft, Leonard Susskind, Eric Verlinde, Charles Thorne, Jacob Beckenstein … . Implemented in a real device with rigid parameters — in an unusual gyroscope, the ability to move isolated information that is physically presented starting from the quantum level, at the «apple» level and on a cosmological scale across the entire holographic screen today already on a computer simulator demonstrates the possibility of teleporting quantum objects without limiting distance and speed of light. Thus, by isolating a physical object inside the rotor, we move complete information about it along the holographic horizon (screen), while simultaneously converting vacuum energy into electrical energy. The teleportation process can be controlled since a real screen map with information can be obtained by measuring the holographic inertial forces inside the teleportation cabin.

TOE and Holographic Principle
Physics cannot do without postulates. Let us temporarily assume that The Holographic Principle is a working theory and postulate that energy and mass can be represented by bits of information, and one bit of information by a phase of the oscillation. Fluctuations of what?
Suppose this is the phase of oscillations of one one-dimensional cosmic string — some object — the foundation of our Universe. Then, in order to determine the phase of the oscillations, we need to have another oscillation relative to which we can determine the phase of the first oscillation. Moreover, to determine the phase of oscillations of the first string, we must have a constant phase difference of the oscillations of two strings. Then it’s easier to imagine one string closed on itself. On this, the postulation ends and mathematics and reasoning logic (deductive method) work. It is known that oscillations with a constant phase difference have the property of coherence. And coherence and interference is a property of holograms.
So, we correctly admitted that the Holographic Principle can be a working theory. Thus, we postulated the need to have a pair of one-dimensional cosmic strings, and their phases are bits of information. In order for our Universe to have a spherical surface with the information that the Holographic Principle insists on, it is enough to assume that a pair of cosmic coherently oscillating strings are, firstly, spirally twisted, and secondly, they must intersect at an angle to each other. At first, it can be any angle, but since the maximum volume is limited by a spherical surface, then the angle of the closure of a pair of strings is 90 degrees. We got a growing sphere surface with bits of information on it.
We check the idea on a computer simulator and with surprise find that the maximum number of oscillation options for pairs of cosmic strings is 64. And the dynamics of the projections of each string demonstrate the numerous properties of elementary particles of the Standard Model! In the center of the projections, we get a beautiful geometric group E8’s. Not a single bit of information on the sphere we have received is lost. Sphere — а bubble without thickness grows with each winding of cosmic strings. Information on-screen is stored without loss and the area of our sphere is growing, in addition, we have exactly two halves of one sphere with slightly different information (since the angle at the beginning we did not 90 degrees). These are known initial conditions in the Universe. Two cosmic strings move strictly along their own of two halves with different information, which means that a force arises in the center of the projections of the strings inside the sphere.
G. ‘t Hooft: «The Standard Model of the sub-atomic particles was established partly by doing experiments with elementary particles and also by imagining “How should these particles behave?” It makes sense to use as an assumption: every particle behaves in a completely deterministic way…».
We can postulate the rejection of the probability density and probability in general as a positive function of the amplitudes of the two projections of the same particle. On the ontological basis, they remain unchanged all the time, then we can idealize the demonstration of two projections of one particle with one equation of coherent oscillations and get two halves of a spherical holographic screen — the attributes of the Holographic Principle. To implement a transformation that turns a quantum system into such an unrecognizable form, a set (N) of unitary rotations of points of pairs of one-dimensional spiral cosmic strings we can realize geometric representation of particle projections for the QM Universe, built by combinations (all 64 options) from one parametric equation. The wave function takes exclusively values 1 or 0 (sinθ, — sinθ, cosθ, -cosθ) and is a qubit:
{θx=Cosθ
Ψ= {θy=Sinθ
{θz=-Sinθ,
If wave function value is a qubit: ψ= this implies that Only then do the attributes of the Holographic Principle appear: a single coordinate of time, two halves of a screen, a pair of projections that characteristically move along two halves of a spherical inflationary surface without thickness. Screen… — all the hidden parameters that physicists have been talking about for so long. In the photo, θx, θy, θz are the sequential angular displacement of the points of pairs of one-dimensional closing spiral cosmic strings. Parameters: θ = πt and -1 ≤ t ≤ 1; where θ is a geometric angle determined by an arbitrary direction clockwise and/or counterclockwise, starting from the corresponding semiaxis of the emerged three-dimensional coordinates. The equation is applicable for any radius of the spherical holographic screen. «t» is the only time coordinate; N as the number of cycles or qubits (bits on the screen that appears). Then indeed, the law of evolution formally consists of elements of the permutation group as qubits can be entangled with each other. In general, the wave function (in the photo) represents the state of the qubit, which differs from the usual representation, because it is not the amplitude of probabilities and can take only on specific values.
The entire screen uses the same time coordinate. Helicity this property of two strings as a third common bit — of information, the reason we perceive the world as three-dimensional. For us observers (as bits are spreading across the screen), this information changes as a result of the accelerated expansion of the screen — these are the relative coordinates of each point in the emerging three-dimensional space-time. The information recorded without loss on the screen with a single current coordinate of the time (t = 0) and with which a pair of projections interact is an illusion of the past time. Thus, the processing of microscopic data on the screen can be naturally performed using signals that pass without a time delay. At the center of the projections, as a result of their movement, at any point inside the sphere, due to different interactions with different information, which from the point of view of thermodynamics can be compared with the temperature gradient on each of the halves one screen, an entropic force arises. We see that the principle of Mach naturally came into play in our Universe.
This super force can be both the mass of particles and energy and the three known forces and the fourth — the gravitational force depending on the scale of consideration of their interaction on the holographic screen when moving each string. In other words, it all depends on how we register these forces — on each of the halves of the screen or on its individual sections (in two, three dimensions or in a multitude). As we see, in the Universe we received and in which, not a single bit of information is lost, there is no place for random processes. There are no measurements, only fixing the results of the movement of information by observers. Superdeterminism is the foundation of our Universe.
So, the most important assumption is that the information associated with a certain area of three-dimensional space obeys the conservation law it — the basis of the Holographic Principle. Information about the location of particles is stored in discrete bits on two halves of the spherical screen — one bit in the Planck-l² areas, but already two Planck areas contain three bits of information as additional information about the coordinates of each of the bits on the screen and are generated automatically. In other words, two bits contain exactly one bit of mutual information.
These types of information bits can accordingly be divided into the image kinetic and potential energy. Whatever information they contain, they contain it together. All information on the two halves of the spherical screen — the closed surface of region A we can be divided into numbers associated with the coordinates of the screen by number N and information represented by the temperature of the screen T. Suppose the system has full energy E. Suppose that this energy is evenly distributed between two halves of one spherical screen with a number of bits N (½kBT as the average energy per bit, where kB is a constant Boltzmann). Then we can determine the temperature T and the number of bits on the screen:
E=N ½kBT
N= A/l², where l² is Planck area = hG/c³
Where G is a universal gravitational constant, c is the speed of light, and h is the given Planck’s constant. Then:
N=Ac³/Gh
Taking a holographic screen as the sphere of radius r, the surface area will be equal to:
A=4пr²
The effective temperature resulting from the equivalent acceleration in the vacuum field according to Unruh effect is:
Т=ha/2пckB
Where a this is the acceleration, which for mass m rotor will be assigned to force F — under Newton’s second law:
F=ma
Newton’s world gravity law:
F=GMm/r²
From the algebraic replacement of forces and the above-mentioned ratios, we will get a known Einstein equation:
E=N½kBT=
=N½kBha/2пckB=haN/4пc=aпr²c³/Gпс=ac²r²/G=Mc²
Thus, for our holographic Universe where every bit carries energy (N — pair of entangled bits — b according to the Landauer Principle):
E=bkBT=Mc².
The appearance of an additional factor is consistent with the hypothesis of dark energy introduced into the mathematical model of the Universe to explain its observed expansion with acceleration. In 2014, data from the BOSS (Baryon Oscillation Spectroscopic Survey) project showed that, with a high degree of accuracy, the value of dark energy is constant in time and space. In addition, these data are consistent with the model of a flat Universe. Flat in the sense that throughout its entire length space can be described using the usual Euclidean geometry. This is the same consistent with the idea of the Holographic Principle with its projections of phenomena in three-dimensional space without loss of information on a flat surface — the holographic screen… .
My invention — the conceptual device — an unusual gyroscope MGGF. This is hard to believe, but his work is based on the two principles: the Holographic Principle and of the principle of least action. These fundamental principles in physics and this mean that in the concept of structure and algorithm of the device — the degree of freedom is severely restricted. And so far unusual gyroscope has not done for two reasons. Firstly, without sophisticated computer technology, it is not possible to make the spherical rotor in a vacuum that will be moved around three axes per cycle under the control of a computer (all according to the same formula of coherent oscillations). Secondly, it is not clear why this is necessary and how it is applied. The gyroscopes very interesting devices and had been speculation that this to do with gravity. It turns out that of all the theories of gravitation is only one theory — the Holographic Principle clearly and surprisingly describes in detail the work of my unusual gyroscope. Moreover, the algorithm is very unusual gyro complements the Holographic Principle. Becomes clear how and why the work thermodynamics (entropy forces) on the surface, what value has the global temperature anisotropy of the surface Universe for dominated of long-range gravitational forces, and more. A very important point.
The Holographic Principle does not postulate long-range gravity, as do other theories, it arises naturally from the holographic scenario. And most importantly, what it is also hard to believe, but the generation of gravitational forces leads us to exchange (transmit and receive) information without limiting the speed of light. If in the Universe there is reasonable civilization they will use it this channel of communication. All these features do not violate a single fundamental law. On the contrary, these laws themselves can be mathematically derived from the laws thermodynamics on the holographic surface. All that I have written, it is the top of the iceberg. Of course, everything looks only conceptually simple, but it may be different. Only an advanced civilization can take advantage of this technology. It remains to find a way for the implementation of MGGF.
«Modular Generator of Gravitational (entropic) Forces» (MGGF)
«Modular Generator of Gravitational (entropic) Forces» (MGGF)
MGGF is designed as an unusual gyroscope. The principal difference between an MGGF any power gyro is that its rotor rotates around three axes and at the same time around a fixed point — the center of mass per cycle. The computer system of control consistently produces an angular displacement of any previously selected point on equator and two meridians of spherical the rotor to the laws of sine and\or cosine. Artificial, forced vibrations of the rotor of MGGF produce are coherent oscillations of his points in space and time. By loading the equations of motion (all 64 directional variants) of any point of the rotor of an MGGF into a computer simulator, we can explore the dynamics of oscillations (trajectories, angular velocities relative to the center of the fixed axes of Cartesian coordinates). The data from the computer simulator demonstrate the surprising connection of the dynamics of any point of the rotor of an MGGF with the statistical dynamics of the projections of elementary particles of the Standard Model (numerous properties obtained at accelerators are observed). One of the main provisions of quantum mechanics is that microscopic particle in their behavior exhibit wave properties. From the standpoint of classical physics, we are talking about coherent oscillations of the points rotor of an MGGF (the angular displacements of rotor points according to the laws of sinus and cosine too are waves). Then for microscopic particles, we are talking about probability waves, which are also known as «the wave function». It is this idea that is incorporated into the Schrödinger equation. For the probability waves, like any other waves, all the same, effects associated with the possibility of imposing waves on each other are also characteristic. This overlap is called «coherent superposition», and this connection of coherent oscillations in classical and quantum interpretation demonstrates an MGGF.
Innovative cycles in the emergence of fundamentally new types of gyroscopes last for a period of forty to fifty years, and the change from one to another occurs only after a serious breakthrough in physics and technology. Gyros can measure the course of a scientific revolution.
Today offered a fundamentally new type of power mechanical (astatic) gyroscope. Spherical rotor with magnets performs forced coherent oscillations of its elements of the mass in a vacuum cavity of a stator with solenoids under computer system control. The device can decide the problems of тeleportation of physical objects, converting vacuum energy into electrical energy and generating entropic forces for move objects in space and on Earth (not a reactive way).
The extremely simple formula of coherent oscillations of the rotor unusual gyroscope in a computer simulator demonstrates the dynamics of the projections «zoo» of elementary particles of the Standard Model, generation the verified multiple experimental data, which are obtained by great efforts at accelerators. We can see the connection with data obtained in the fields of Quantum Physics and the Holographic Principle. How does the device work?
De Broglie waves are waves of probability amplitude. Coherent oscillations of the rotor leading to the appearance of a fixed interference pattern from the accelerations of massive particles and an increase in the amplitude of the probability that a particle is detected at a given point in space thus a fixed and directional force acts on each particle and dictates involvement of in the interference pattern. «At interference, the wave energy is redistributed in space. This does not contradict the law of conservation of energy because on average, for a large region of space, the energy of the resulting wave is equal to the sum of the energies of the interfering waves» — Wikipedia.
In condition isolation thermodynamics system by vacuum from the external environment, energy coherent oscillation converted into mechanical energy and right there in electrical energy (in mode recuperating, magnets of the rotor induced emf in the stator around two of the three axes rotation per cycle). We can have the converted double the thermodynamic free environmentally clean energy into electrical and use simultaneously an unusual gyroscope as a generator of long-range entropic force obtained in all 64 variants of the direction of coherent oscillations. The new experimental data: a rotor weighing only 50 grams at a speed of 7,000 rpm in vacuum generates a long-range entropy force of 2,7N.
This does not contradict the fundamental conservation laws energy and impulse since the size of a closed system with coherent oscillations particles limited to the holographic screen itself. This new holographic technology can be expanded to a meaningful scale it could portend a revolution in the science, industry, households will receive free Zero-point Energy without electric highways. Energy wars stop. Spacecraft would no longer need tons of propellant to stay in orbit or explore deep space.
Abstract
A system and method for controlling moving artificial or natural of objects in space in any direction produce under the action created gravitational forces. Embodiments achieve spherical motor this moving and stabilizing with a gyroscope — spherical motor (system spherical a rotor inside a vacuumed cavity of a spherical stator). The spherical motor system comprises a spherical rotor having permanent magnets arranged in evenly-spaced antipodal pairs in a lattice form with polarities of adjacent magnetic poles differing. The spherical motor system also comprises a stator which has optical and magnetic sensors surrounding electromagnets. The spherical motor system further comprises a computer system that controls the timing and duration of energization of the electromagnets based on the detection of one of the permanent magnets by the magnetic and optical sensors for to control the position of the rotor and his coherent oscillations. Such a spherical motor system provides three-axis stabilization and moving control of a satellite or natural objects another vehicle meteorites, asteroids, comets in the space under the action of artificially obtained gravitational forces in a non-reactive way.

Image 1. Rotor



Image 2. Stator base — half


Image 3. Vacuum cavity a shell (of a stator) that surrounds the rotor

Image 3. Solenoid and five magnetic sensors

Image 5. Design.
1. Base.
2. Enclosure.
3. The Stator (diameter front section).
4. Frame.
5. Rotor.
6. Magnets.
7. Magnetic point (one of the magnets, as an exception, is not displaced).
8. Vacuum cavity (diameter front section)
9. Solenoids.
10. Sensors optical.
11. Slave controllers and drivers of induced coils.
12. Computer.
13. Accumulators.
14. Solar batteries.
15. Retaining bolts.
Classifications
BACKGROUND
For quite a long time, the concept of construction is known for controlling the motion of a sphere with magnets along three axes inside another sphere with inductances. Below are several papers and even a patent describing the general concept of using a spherical engine to control a spacecraft. See, e.g., U.S. Pat. No. 4,611,863, entitled, “Magnetically Supported and Torqued Momentum Reaction Sphere,” William Isely, Issued Sep. 16, 1986, PCT Patent Application WO 2007/113666 A2 entitled “Reaction Sphere for Attitude Control;” and NASA SBIR Phase 1 Noqsi Aerospace, Ltd. “A Reaction Sphere for High-Performance Attitude Control,” study completed Dec. 10, 2011,
Reaction sphere for stabilization and control in three axes» US9475592B2 2013-01-31, all of which are hereby incorporated by reference. None of these documents present a workable spherical motor solution for сhange in orbit inclination, movements, and stabilization of satellites or other vehicles using artificially created gravitational forces. All of these documents teach considerably different control theories and fundamentally different from the one proposed below new type of power gyroscope based on coherent oscillations of the rotor.
SUMMARY
Embodiments are directed to a spherical motor system for control moved, stabilization of a vehicle in three-dimensional space. The system comprises a spherical rotor having permanent magnets positioned in evenly-spaced antipodal pairs. Each of the permanent magnets is oriented with the magnetic pole facing outward from the center of the rotor and in a checkerboard pattern approximately uniformly mounted over the entire spherical surface of the rotor. The system also comprises a stator having solenoids positioned in evenly-spaced antipodal pairs that spatially correspond with the permanent magnets. The stator further has optical sensors under each solenoid, four of which are located under the solenoids at the edges (cross). See (Image 3). The system further comprises a computer control system that controls the timing, direction, and duration of energization of the solenoids based on the detection of any of the permanent magnets to provide the solenoids with the necessary magnetic pole in order to attract or pushing off permanent magnets axially or radially order whereby momentum is transferred between the rotor and the stator along a controlled vector.
In an embodiment, the rotor comprises non-magnetic material between the permanent magnets. The non-magnetic material may be selected from the group consisting of plastic, aluminum, 300-series stainless steel, tungsten, or ceramics.
The optical analog sensors used to determine the position of the rotor relative to the stator.
In an embodiment, the vehicle may be a satellite, wherein the stator is connected to the satellite.
Embodiments are also directed to a method for controlling and stabilizing a vehicle in three orthogonal axes and\or in any of the 64 directions of three-dimensional space. The method comprises similar features that correspond to the above-mentioned system.
Detailed description
Theory and experiments
Any physical theory exists if it is in practice repeatedly confirmed in experiments. This also applies to the fundamental theory — the Holographic Principle. We can demonstrate the viability of this idea first on the simulator, downloading the extremely simple equation of coherent oscillations into it, and then on a real mechatronics device — on an unusual gyroscope — MGGF.
According to Euler’s rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible. However, for of full turnover of a physical body simultaneously around a fixed point and around three fixed Cartesian axes per cycle — possible. For is we can use one a simple parametric equation of angular displacement any the points on the meridians and of the equator of the spherical rotor around fixed Cartesian axes according to the laws of simple harmonic motion.

So the unusualness of the gyroscope is justified by the fact that its spherical balanced ceramic rotor in a vacuum per cycle produces one complete revolution not around one axis as in conventional power gyroscopes but simultaneously around a fixed point — the center of mass and three axes according to the laws of harmonic oscillations and so it has fundamentally new properties. Forced oscillations of the rotor of unusual gyroscope posses spatial and temporal coherence since the phase difference of the orthogonal oscillations of every point of the rotor is constant. More generally, coherence describes all properties of the correlation between physical quantities between several waves or wave packets and generate a fixed interference pattern. For coherent oscillations of the rotor, this a fixed interference pattern is six group of angular accelerations elements of mass in vacuum connected with directed of the fixed axes of Cartesian coordinates. It is assumed that the artificial displacement of the interference pattern causes the decoherence and result in a directed and distance-acting entropic force. The result of the operation of an unusual gyroscope is the possibility controlled of generating directed entropic forces, which leads to controlled entropiс gravity, also known as emergent gravity.
Natural levitation as the first step to control gravity.
Experiment 1.
If we quickly rotate, for example, the disk in a vacuum, we can observe the action of entropic forces repelling the driven disk. The effect independent of the material of the disks, but depends on the angular accelerations of the drive disk and the degree of vacuum (residual air pressure in a chamber). Discs do not touch each other when interacting.
This video demonstrates the non-electromagnetic, non-electrical and non-magnetic interaction of rotating non-magnetic disks. We can assume this acceleration of the elements of mass in a vacuum causes significant entropic force. V. N. Samokhvalov “Non-electromagnetic Force Interaction in Presence of Rotating Mass in Vacuum,” [24].
Since all forces, according to the Holographic Principle, can be reduced to entropic forces in a vacuum (the temperature of two disks increases with interaction), we can suggest that for an unusual gyroscope, this means that after its rotor is untwisted to the appropriate speeds in a vacuum it does not need to maintain its forced levitation and it will naturally levitate inside the stator.
Judging by the results of experiments this is not an electromagnetic interaction at a distance when the masses rotate in a vacuum. To an unusual gyroscope has a direct relationship because we observe the action of significant long-range entropic forces in a vacuum. If we rotate a spherical rotor in a vacuum around three axes per cycle in the stator cavity, then the levitation of the rotor will occur without the need to artificially support it. And, most importantly, the accuracy of the coherent oscillations of the rotor self-organizes when the rotor is naturally repelled from the inner walls of the stator. This co-operative quantum effect and the accuracy of performing coherent oscillations are of great importance.
The graph shows the rotational speed of the driven disk (50 grams), depending on the degree of vacuum and for two values of the supply rotational speed of the master disk (supply voltage of the engine: black point — 27 volts, red — 30 volts).
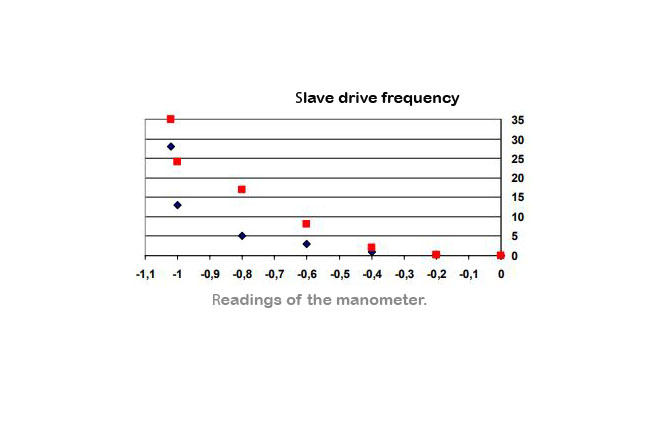
The effectiveness of the action of forces at a distance is clearly seen, depending on the degree of vacuum.
This is another experimental proof of long-range entropic forces: 2,5 . . . 2,7 N, and we have unique properties of an unusual gyroscope generated the directions of the entropic forces from the coherence oscillations of the mass in a vacuum.
TOE and unusual gyroscope 6DoF
If we this begins the Theory Of Everything (TOE) on the base of, the Holographic Principle, then first we need to show how the whole zoo of the particles of the Standard Model arises from one that looks infinitely simple equation coherent oscillation. This the tool — the same equation which we used to control the oscillations of the rotor of an unusual gyroscope and that exactly reproduces quantum mechanics and together emerges on the spherical holographic surface — screen. Besides, we have a certified (repeatedly verified by independent experts) simulator, in which we establish this simple equation and get a correspondence with the properties of many known quantum particles of the Standard Model obtained on accelerators. We need to emphasize one equation — and we can have watched the properties of many particles, not just one electron, for example. The equation obtained and experimentally verified in this way is a coherent law of evolution. As a result, we can explain how information is encoded on a holographic screen, the fundamentals of thermodynamics, respectively, we can obtain the entropic force — root all known four forces (including gravity force), we have of mathematical derivation of the fundamental laws and prove Holographic Principle. Moreover, these conclusions can be experimentally confirmed and by another method in the real device — an unusual gyroscope whose coherent oscillations of the rotor are described by the same equation. In addition to as an instrument for research in the field of quantum physics and cosmology, an unusual gyroscope can be used as part of a propulsion system for applications associated with the creation of the artificial forces of gravity (AFG).
In this paper, we that will determine main theoretical and practical aspects of technology unusual gyroscope for the practical use his as a new instrument for research in the field of quantum physics, cosmology and of an as the device for creating AFG.
We present an innovative method for generating entropic force using an unusual gyroscope. Measurement of the entropic force along with methods based on charged particle accelerators can be used to study the properties of particles of the Standard Model. The generation of entropic force can be used in cosmology to study the parameters of a holographic screen in real time. The entropic force received in an unusual gyroscope possesses the properties of gravitational force — AFG a «far-off effect» and can be used in various applications as a propulsion system for vehicles both in Space and on Earth, without violating the fundamental laws of physics.
First, we need to demonstrate the possibility of creating coherent oscillations of any point in three-dimensional space from extremely simply the parametric equation and demonstrate these oscillations on the simulator.
Extremely simple parametric equation of spherical motion
We need to demonstrate the possibility of creating coherent oscillations of a dynamic system (a spherical rotor in an evacuated cavity of a spherical stator of an unusual gyroscope). The equation includes a complete set of variables determining the state of the system in three-dimensional space (coordinates, velocities, and pulses), as well as their time derivatives. Using the process, one can choose Δt sufficiently small, but finite to obtain an approximate numerical solution of the equations of spherical motion.
In modern quantum theory, the term equation of motion is often used to designate just the classical equations of motion, that is, just to distinguish the classical and quantum cases. In this case, the use of the word “solution of the equations of motion” means precisely the classical (nonquantum) approximation, which can then be used one way or another in obtaining a quantum result or for comparison with it. We call the parametric equation — the classical equation of motion os analog equation of motion of a spinor field.
The spherical rotor in a vacuum makes forced oscillations under the control of a computer. Each point of the rotor moves along many surfaces of concentric spheres around one fixed point. We can compare these points with the elements of the rotor mass.
Let us start with the definition of coherent oscillation of a classical body.
“The motion of a physical body when only one its point О remains fixed all the time is called the rigid body motion (rotation) around a fixed point О. In this case, all points of the physical body move along the surface of concentric spheres, the centers of which are located in the point О. Therefore, such motion is called the spherical motion of the body. Based on the definition of the spherical motion, we obtain parametric equations of the coherent oscillation of the elements of mass ”.
«The coherent oscillations of the mass elements are spherical motion of a physical body, the forced total harmonic oscillations of which are sequentially performed of triads, each time by the angular displacements of its points at the intersection of the axes of fixed Cartesian coordinates with concentric spheres, and change per the cycle according to the law of cosine and\or sine.»
(θx=Cosθ
(θy=-Sinθ
(θz=Sinθ
θx, θy, θz — angular displacement of previously selected points on two orthogonal meridians and the equator of the spherical rotor’s, around orthogonal to their flatness the corresponding fixed Cartesian axes associated with the accelerated observer.
Parameters: θ = πt and -1 ≤ t ≤ 1; where θ is the geometric angle defined by an arbitrary direction in a clockwise, starting with the corresponding semiaxis, and t specifies the required accuracy of the angular displacement. When Δt → 0 and are the coordinates of the center ε → 0.
We have an extremely simple equation of the rotor spherical motion of an unusual gyroscope in three-dimensional space.
Slow simulation of coherent oscillations of a sherical rotor on the parametrical equati
A very slow-motion video shows a cycle of three-dimensional rotations of a spherical rotor of the unusual gyroscope — the result of computer modeling of coherent oscillations of its points (mass elements). The dynamics of the rotor is built according to a single and extremely simple formula of angular displacements of its points at the equator and two meridians according to harmonic laws. The resulting image looks a bit like a Maltese cross, just like the wave function predicted from Schrödinger’s equation.
For 3D simulators, only storing a matrix of 60 spins will require about a few terabytes of memory.
But it is impossible to effectively simulate the dynamics of quantum particles because of the appearance of a formally negative probability. Since this problem is seen by a scientist as fundamentally irresolvable, a complex nonequilibrium system will not be able to calculate any power on a computer in a finite time. But if we postulate the positive probability itself and write it in the form of a parametric formula, we can see the dynamics of the particle projections on a spherical screen and study their properties.
Already today, the new method a worked based unusual gyroscope proved to be a valuable tool to provide dynamic and quantification of the property of particles of Standart Model. The computer simulator «IsAN» for experimental verification of the Holographic Principle allows working on the Planck scale, about 10-33 cm, which is more than a billion times a billion times less than anything that can be studied directly with laboratory experiments.
At the heart of the Universe is anisotropy — a global temperature gradient. Suppose that the Holographic Principle works, and then this gradient of temperature can be projected without loss of information on the spherical holographic screen. Then the pairs of projections (entropy gradients, known in quantum mechanics the phenomenon called «zitterbewegung») moving along on the chosen each of half-screens, according to thermodynamics, will interact with the global temperature gradient and experience various entropic forces.
We can assume the choice of the half of the screen through which the particle projections move is negative feedback, which naturally limits the range needed to fine-tune the parameters in the Universe (natural auto-tuning defined values of fundamental constants). Under the conditions of coherence for the projections of quantum particles, this entropic force gives mass to the particle itself (gravitational charge).
On the screen, we can see three generations of particles, the intersection of their projections on the screen, which can explain the known three forces and interactions. In the classical world, under the conditions of decoherence, the entropic force is a gravitational force — a cooperative phenomenon. Many such forces are what we call entropic gravity. This formalism solving the problems of hierarchy additionally demonstrates the difference between the mechanism emerge of the inertial and gravitational mass, which can manifest itself on a large scale and explain the presence of dark matter. Example, entropic gravity posits that what has been interpreted as the unobserved dark matter is the product of cooperative quantum phenomenon that can be regarded as a form of positive dark energy that lifts the vacuum energy of space from its ground state value. A central tenet of the theory is that the positive dark energy leads to a thermal-volume law contribution to entropy that overtakes the area law of anti-de Sitter space precisely at the cosmological (holographic) horizon.
Note that the curvature of space-time (3D) is not required since it is secondary if we are in the position of a Holographic Principle. Space-time and gravity emerge together with fundamental laws on a holographic screen (2D), as a three-dimensional image on a film of an optical hologram. It is appropriate to recall that in connection with this favorite weapon of physicists is Occam’s razor. Common sense tells us that only a film is real, and a three-dimensional image is an illusion. However, in daily life, nobody will suffer from the consequences of such an observation it pertains to the deeper fundamental nature of physical laws. In the video image of the projection of the particles of the Standard Model, the pairs move along the holographic screen, on which we can design this photo of the global temperature gradient. Projection centers — particles experience different (but in each cycle of quantum measurements — the constants) entropic forces.
Simulator «IsAN» is a video made by one extremely simple equation of coherent oscillations.
Introduction
Today, the Holographic Principle — is hundreds of theoretical works by famous world-class physicists: G. ‘t Hooft, L. Susskind, J.D. Bekenstein, E. Verlinde, J.M. Maldacena, R. Bousso …. . Already there are experimental studies confirming the operation of the Holographic Principle [30], [32][36] . Since 1997, more than 10,000 works have been published supporting this idea.
According to the Holographic Principle: our world does not have 3+1 dimensional. The observable degrees of freedom in the Planckian scale can best be described as if they were Boolean variables defined on a two-dimensional screen, evolving with time.
Understanding of the emergent nature of space-time and gravity comes from the laws of black hole thermodynamics and the Holographic Principle was born after expansion of the laws thermodynamics for the surface all Universe. Bekenstein [7] have suggested a deep connection between gravity and thermodynamics. Through several decades of research and experimentation, physicists have brought forth a unified theory of the Universe that is based on information theoretic principles. The Holographic Principle states that the entropy of ordinary mass (not just black holes) is also proportional to surface area and not volume; that volume itself is illusory and the Universe is really a hologram which is isomorphic to the information «inscribed» on the surface of its boundary horizon — holographic screen.
The complexity of physical theories based on a Holographic Principle, for example, research at the level of quantum particles of the atomic nucleus and electronic shells, requires the creation of an effective spatial model of a computer quantum simulator for testing, example, Theory of Everything (ToE) but even this is not enough. Because the relevant distance scale at which fundamental modifications of our present theoretical views are expected to be needed is the so-called Planck Length, some 10‾³³ cm, which is more than a billion billion times smaller than anything that can be studied directly with laboratory experiments. However, for a tandem approach — experimental of measurements of the cooperative quantum phenomenon and visualize quantum processes on the basis of an electro-mechatronic device — unusual gyroscope and computer quantum simulator «IsAN» of the dynamics of the projections (subcomponents) of quantum particles this may be possible. If the Holographic Principle works, we can get an uncompensated entropic force applied to the center of mass of the rotor of an unusual gyroscope. According to the conclusions of the Holographic Principle, this entropic force is equivalent to the gravitational force. A series generated by directed gravitational forces lead us to controlled gravity. The directional entropic force can be obtained by shifting the coherent oscillations of the rotor of an unusual gyroscope and is a result of the interaction of global temperature gradients on the holographic screen of the Universe and entropy gradients caused by angular displacements of the projections group element of the mass. This entropic force can be measured (read) in real time.
Emergent holographic two halves spherical screen
Modern researchers consider the line as one-dimensional space. As soon as the zero point is placed on the line, as the origin, this means in engineering language the binding of this line to the real space. However, in this case, eliminating even one the point 0 from the set, to name a line «the one-dimensional space» means to violate the law of preservation of information of the Holographic Principle.
Therefore, if on the line it is required to consider a transition along a line from -∞ to a point 0 and to + ∞, then it is necessary to turn around the point 0 along the arc ε and make a rotation through the angle Ѳ = ± π.

If we ignore this fact, calling the line a one-dimensional space, then it means breaking we law of preserving the information of the Holographic Principle and, consequently, making a mistake in the foundation of physics. If we accept the impossibility of losing information as the basis for describing the world around, then it is necessary to accept the fact that the line has a discontinuity at the origin, regardless of the minimum radius of the arc ε → 0, but now this can not be called a one-dimensional space.
Next, we consider the steady-state concept of a two-dimensional (flat) space. If the plane is drawn without the origin, then this concept does not bear physical meaning. If the plane is tied to real space, then the origin of coordinates is fixed in it. In this case, the logic of the previous reasoning takes effect. The neighborhood of zero does not belong to this two-dimensional world. The neighborhood of zero is a punctured point in a two-dimensional space. Definition, zero physically means that the plane is punctured by a ray or projection emanating from another emergent dimension. This the paper also asserts that the plane carries an element of the emergence of space within itself, and this is confirmed by the Holographic Principle itself, and this statement is its basic content. In this process, the transition to other large-scale measurements ends, because according to the Holographic Principle, really there is only one surface with information — the holographic screen of the Universe. Thus, continuing the transition to the plane from -∞ through the point 0 to + ∞, we must again circle 0 along the arc ε in order to make a rotation through the angle Ѳ = ± π. Likewise, as we circled the point 0 on the line, on the plane we can additionally rotate the coordinates around the point 0, therefore each arc ε will describe the hemisphere.

If we now direct the arc radius to zero (ε → 0), then on the quantum level there will be a rotation through the angle Ѳ = + π or Ѳ = -π, and on the pole of the emergent sphere there will be the interaction of the particle with the measuring device (and/or with temperature gradient), which fixes the value of classical physical values and the distribution of their probabilities. In our holographic Universe, this is determined by the fact that two diametrical pairs of points on a spherical screen project one point in the emerging three-dimensional space with the Euclidean distance definition. This formalism demonstrates the inextricable connection between particles — waves and particles — points.
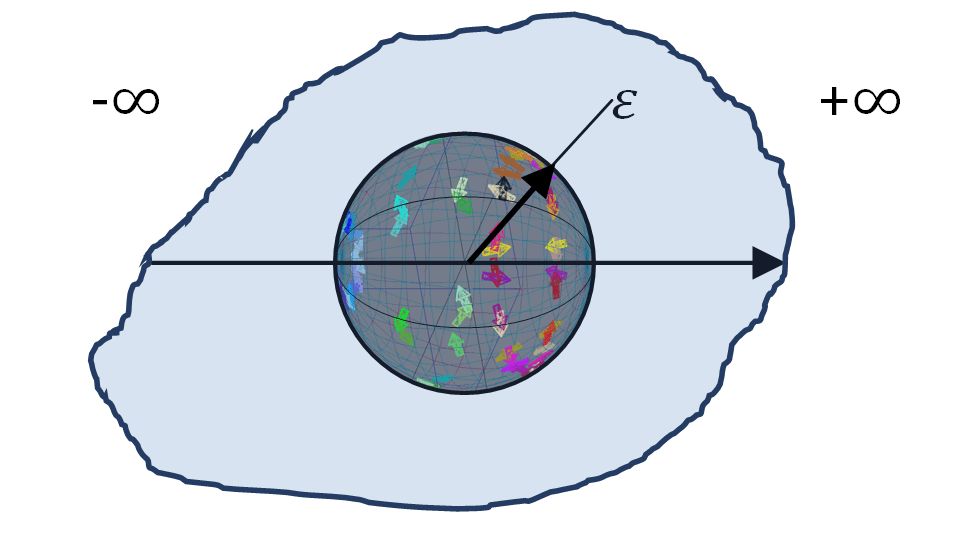
Holographic principle, based on the law of information preservation, allows the projection of any phenomenon onto the holographic screen of the Universe and roundtrip without loss of information. Therefore, naturally, the sphere in every point of space 3D we have obtained is considered on the holographic screen 2D of the Universe. It becomes clear why the fundamental laws of physics are related to the square of the radius.
With such a geometric and physical interpretation of the abstract concept of a point is are detailed: each point of emerging three-dimensional space the center of two projections and the statistical angular movements projections of the particle in a natural way (from a simple equation of coherent oscillations) emerge on two hemispheres — is a wave.
In quantum mechanics, particles have internal degrees of freedom, which, under thermodynamic isolation, are not related to the motion of the particle as a whole. The statistic dynamics of the particle projections may be demonstrated of trajectories on the simulator. The evolution of such a thermodynamic system is represented by classical angular movements that «survive» on the screen as a result of the interaction of the particle projections between themselves and the global temperature gradient and this process we can visualize in the quantum simulator «IsAN».
The natural coding of the laws of physics on the holographic screen determines the fundamental character of the holographic principle itself. This means that we can generate a directed entropic (gravitational) force in an unusual gyroscope with six degrees of freedom and visualize the statistical dynamics of the fundamental particles of the Standard Model from one simple formula.
This video should be supplemented by a global temperature gradient and will be complete and we immediately can turn on thermodynamics. We show that in such theory, naturally, observe emerging on spherical the screen the 60 pairs of projections, each of which is defined as a particle. Which exactly half of the screen will be involved depends on the measurement. There is a global negative connection (loop) and this formalism of negative feedback solves the problem of certain values of fundamental constants. Such a formalism in dynamics can explain the reasons for the self-organization of the projections (subcomponents) of elementary particles, leading to the emerging of mass and color charge. For such a model, the matter appears to be already included in the microscopic kinematics and dynamics.
On the simulator «IsAN» after loading a parametric equation describing one cycle of coherent oscillations, we observe the statistical dynamics of projections of fundamental particles of the standard model onto a spherical holographic screen of arbitrary radius (antiparticles are excluded from consideration). We can see the mathematical the coherence of quantum mechanics.
We take any point in space and it is compatible with the center of fixed Cartesian coordinates and simultaneously with the center of a sphere of arbitrary radius. We divide the time into equal intervals.
Postulate: «If the quantum probabilities are not only preserved, in the ontological basis they stay the same all the time then we can idealized demonstration them by the single equation of coherent oscillations. We can define probabilities to be a positive function of the amplitudes».
In the quantum simulator «IsAN» fragments of computer calculations of angular movement are shown — a geometrical representation of the probability density of some projections of particles constructed by combinations of coherent oscillations from one parametric equation or qubit emerge of a coherent evolution law:
(θx=Cosθ
N (θy=Sinθ
(θz=-Sinθ
N-number of cycles; θx, θy, θz- sequential angular displacement of projections on the holographic screen. θhs — sequential angular as the result coherent oscillation of the holographic screen. Parameters: θ = πt and -1 ≤ t ≤ 1; where θ is the geometric angle defined by an arbitrary direction in a clockwise and/or counterclockwise direction, starting with the corresponding semiaxis. The equation is applicable for any radius. When t → tp — is the Planck time. are the coordinates of the center and ε → 0.
tp -is the Planck time.
The small-angle approximation is a simplification of the basic trigonometric functions which is approximately true in the limit where the angle approaches zero. They are truncations of the Taylor series for the basic trigonometric functions to a second-order approximation.
sin(θ)≅ θ
“In the limit of a very large region, the bonding surface can be taken to be a flat plane at infinity». Then рrojections on holographic screen H = A=∞, S — Arc length — the path of the projected point and O — Line segment on a holographic screen. Then S = O, θ∼S and
sin(θ)= θ.

The equation is valid for any radius of a spherical screen.
We postulate that the limit of the number of cycles of coherent oscillations per second is the limit, in real quantum processes. When we are dealing with the Plank’s angular frequency defined in terms of fundamental constants in natural units.
The Plank’s angular frequency is defined as the inverse of the Plank’s time (tp) expressed in seconds (s). Taking this into account, for the Plank’s angular frequency — the number of cycles of coherent oscillations per second (ωp):
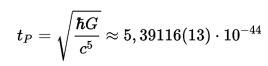
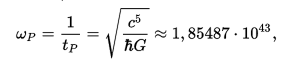
c — is the speed of light in a vacuum,
ħ — is the Dirac constant (Planck’s constant divided 2π),
G — is the gravitational constant,
tp -is the Planck time.
At every instant, the rules lead to one single, unambiguous prescription as to what will happen next cycle equal Plank’s time.
Holographic interpretation of qubit:
G. ‘t Hooft: «The Standard Model of the sub-atomic particles was established partly by doing experiments with elementary particles and also by imagining “How should these particles behave?” It makes sense to use as an assumption: every particle behaves in a completely deterministic way…» We can postulate probabilities as a positive function of the amplitudes two projections one of particle. If the quantum probabilities are not only preserved, in the ontological basis they stay the same all the time then we can idealized demonstration two projections one of the particle by the single equation of coherent oscillations and get two halves the spherical holographic screen. Geometrical representation of the probability density projections of particles for the QM Universe constructed by combinations of (all 64 variants) from one parametric equation presents of the qubit:
(θx=Cosθ
N (θy=Sinθ
(θz=-Sinθ,
where θx, θy, θz- sequential angular displacement of projection on the holographic screen. Parameters: θ = πt and -1 ≤ t ≤ 1; where θ is the geometric angle defined by an arbitrary direction in a clockwise, starting with the corresponding semiaxis. The equation is applicable for any radius. N-number of cycles or qubits; t → tp — is the Planck time. By loading all 64 variants of coherent oscillations of pairs of particle projections into any program to demonstrate point (vector) dynamics in 3D angular displacements, for example, in “3D Max”, we get two halves of one spherical screen and characteristic dynamics and numerous properties of elementary particle projections of all three generations, from huge efforts obtained on particle accelerators. This Universal Holographic Code of the Universe. A set of qubits entangled among themselves can be interpreted as an emerging space.
The rules according to which quantum mechanics works, are precisely formulated in what is called the Copenhagen interpretation. However, uncertainties lead to the fact that the phase of the wave function is not interpreted in theory and this is in contradiction with the fundamental conclusion of the Holographic Principle that information loss is impossible. Nevertheless, the behavior of a particle can be described as completely as if there were no uncertainties.
A new formulation of quantum mechanics on the base of Holographic Principle is proposed, namely a general definition of the probability of an event on the holographic screen. The physical content of quantum mechanics based on holographic formalism this makes it possible to solve problems without resorting to the use of wave functions and operators.
Postulate. One bit of information is represented by one phase per cycle of coherent oscillations two of the particle projection vector with respect to the global temperature gradient on a spherical holographic screen. The number of directions of coherent oscillations (Number of the angular movements) can be calculated. Each axis of three-dimensional space is connected with two directions of coherent oscillations. Thus, we have six main directions, the maximum number of directions is sixty and four separate directions of coherent oscillations. In practice, what this means is that, when a system is described quantum mechanically, we apply number. One particle about is a bit, two-bit values (0/1) are two projections of a particle.:
4³- 4=60, (±cosθ,±sinθ→4 for 3 coordinates).

Table of qubits

The table does not show four variants from all (60+4, 64qubits) that do not fall under the definition of coherent oscillations (there is no phase shift).
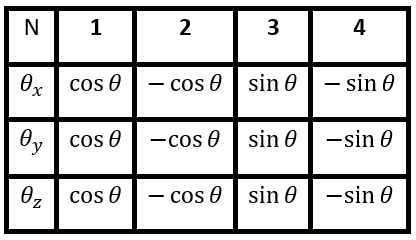
This table can explain the absence in nature of massless particles with zero spins. Photons, gluons, gravitons, neutrinos are massless or almost massless particles (total four qubits).
We identify one bit of information with one of the phases of orthogonal coherent oscillations as the fundamental bit of natural coding of information in one area of the horizon of a spherical holographic screen. According to the Holographic Principle, these classes are distributed across the horizon in such a way that we have one bit of information for each area segment of roughly the Planck length squared.
In the quantum simulator, the arrow — vector indicates on this projection of the particle. In the physical sense, the arrow on the spherical holographic screen is the direction of the local temperature gradient (Planck’s temperature). A pair or more projections of particles in the center of the projections form a simple particle.
Thus, the total number of simple particles in the quantum simulator is exactly 60. The Standart Model of elementary particles describes 61 particles (the last discovered was the Higgs boson).
On the quantum simulator IsAN you can see a picture in which there are pairs of diametrically located projections of particles, which in themselves do not have mass. We give these particle projections the names «Is» and «AN». Being massless projections, they move along diametrically opposite sections of the holographic screen have speed of light, but instead it can be observed on the quantum simulator that they «rock» back and forth on it, and the forward motion of the projection particle «Is» continuously turns into a backward motion of the projection particle » AN «, and vice versa. In fact, this is the realization on the holographic screen of a phenomenon called «zitterbewegung» in quantum physics and consists in the fact that the instantaneous movement of an electron, for example, because of participation in such vibrations, always occurs limit speed of light, although the full the average motion of an electron is characterized by a velocity less than the speed of light. Each of these ingredients has a spin of 1 / 2ℏ in the direction of motion corresponding to the left rotation in the case of the projection of the particle «Is» and the right for the projection of the particle «AN». The real motion of the projections of the electron «Is» and «AN» is composed of a large number of such separate processes so that the observed motion of the electron can be regarded as the result of some «averaging» (although, strictly speaking, quantum superposition takes place here).
After running the quantum simulator on a spherical screen, you see special points — the poles of the sphere and the cluster points, the discrepancies between the projections of the particles. They can be identified as specific interaction points for particles and as nodes for the formation of complex composite particles. For composite particles, some of the projections consist of more complex sets of their angular movements or trajectories. More complex composite particles, in physical terms, have more «windings» of projections on the surface of the sphere of the holographic screen.
To each fundamental fermion, there corresponds an antiparticle with the same mass. All the charges of the antifermion are opposite. Projections of antiparticles moving «backward in time» are also important for research, but they are still excluded from consideration in the quantum simulator.
One of the arguments in favor of the reliability of computer quantum simulation of the dynamics of the projection of particles is its natural appearance from one concise parametric equation of coherent oscillations. The first thing that is observed in the quantum simulator after its launch is the dynamics of the projections of particles of three generations on a spherical holographic screen.
The holographic screen — surface of elementary events is chosen as a set of random “quantum trajectories” of two projects of one particle — trajectories with an arbitrarily changing the arrow of time. Physical events are subsets emerging space as a result of the measurement or in other words — choosing one of two paths (trajectories) on each half of the holographic screen.
It is significant that since time in a generalized quantum mechanics randomly changes sign, there is no evolution in it, but there is movement both in the future and in the past, the arrow of time arises as a consequence of the “interference of trajectories”. Evolution based on the holographic principle encapsulates all laws of physics does and not lead to the loss of information. This is an effective way to encode information without loss on the holographic screen. We emphasize that the existence of the arrow of time is not associated with irreversibility, as opposed to the usual statements. The motion of the quantum system turns out to be reversible, because trajectories “survive” without breaks in time, going both from past to future and from future to past on holographic screen having inflation. The simple act of a measurement sends a signal backward in time (without limiting the speed of light) to another half of the holographic screen of the Universe.
The simulator demonstrates a coherent evolution law and we can see dynamics projects of particles on 2D screen.
These are probabilities associated with the measurement of commuting quantities, in which it is not necessary to take into account the reaction of the instruments. Is the possibility of using (1) allows to carry over accustomed classical ideas into the microscopic world [34]. It was proposed by G. V. Ryazanov in (1958). Allows you to get a quantum-mechanical description, based only on images and concepts of classical statistics. Wavefunction for such a formulation not needed and can only be saved for calculations. As in Feynman’s interpretation, here as an elementary space event is considered a set of trajectories of moving particles their positions 1 to position 2. Along with Feynman trajectories corresponding to the motion reversed along
of time. The trajectories may have loops, in some areas of which the particle moves back in time. Quantum trajectories are described by continuous and nowhere differentiable functions (such functions can be studied, using fractional dimensions and properties of fractal sets). So Thus, the space of elementary events at Ryazanov expands compared with the space of Feynman trajectories. Instead of Wiener’s measure, the alternating measure of Ryazanov has introduced: the probability of passing through this the trajectory is assumed to be proportional to cos (S/h). Such a formalism is confirmed by experimental data obtained on a computer simulator IsAN. The probability particle propagation along the trajectory can be both positive and negative. The introduction of negative probabilities can be compared with the introduction of negative numbers. When summing trajectories, all loops are mutually are destroyed (“the trajectories interference theorem”) and remains group trajectories1 → 2 (“forward”) and 2 → 1 (“backward”). Remarkable in Ryazanov’s interpretation is that the primary concept here is elementary factor events — the transition of particles from state 1 to state 2, but not wavefunction, without which is now can do without. The basic equation is also is the equation for probability. It can be shown that this equation implies the Schrödinger equation and the formulation of quantum mechanics using the concept of wave function Ψ. This interpretation Ryazanov is fundamentally different from all other interpretations, including Feynman’s interpretation. The principle of Ryazanov contains all the whole quantum mechanics: wave function, superposition principle, operators and commutation relations.
The temperature gradient on the holographic screen as hidden parameters.
Postulate. The global temperature gradient on the everybody two hemispheres of holographic screen interacts differently with moved projections of the particles «Is» and «AN», which gives the particles different properties (mass, for example). This mechanism for many different particles of matter, according to thermodynamics on the holographic screen, is responsible for the appearance of the entropic force, which acquires the appearance of all known fundamental forces and interactions.
On the screen of your computer after loading into the quantum simulator the parametric equation «coherent evolution law» «IsAN», we can have:
1. The appearance of a spherical screen, which can be viewed from any pre-selected position.
2. The appearance of two hemispheres screen and move projections of the particles «Is» and «AN» at different speeds.
- Projections of 60particles (plus 4 massless particles) of the Standard Model, their dynamics and characteristic intersection points of their statistic angular movements.
- The characteristic angular movements of particle projections, which we have associated with three generations particles of the Standard Model.
- The angular movements projections of particles are uniquely determined on a spherical screen per cycle. At every instant, the rules lead to one single, unambiguous prescription as to what will happen next. The cycle time can be varied.
6. According to thermodynamics on the holographic screen described below, against the background of the fact that entropy does not decrease (information about past is preserved), the interaction of particle projections with global and local temperature gradients on a holographic screen determines the cause of the events that occur. «We have causality: every event must have a cause, and these causes all must lie in the past, not in the future. A demand of this sort is mandatory. What it really means is that, what is supposed to happen next, we should never be confronted with a circular situation, or in other words, we should always know in which order the rules must be applied. Whatever that order is, can be used to define time. So now we can distinguish the future from past. Only the past events are relevant for what happens next, and whatever they dictate, will only affect the future»[1] [Page 5. 31].
7. The visualization of the interaction with the global temperature gradient (the events in the past) and with other particle projections on the screen demonstrates the effectiveness of the coherent evolution law. «Efficiency. Not all events in the past, but only a few of them should dictate an event in the presence. This suggests that there is a power limitation in we can’t have that every particle in the past, instantly determines the behavior of every particle in the future. If for computing the behavior of one particle, we only need the data concerning a few particles in its immediate environment, then the calculation will go a lot quicker. We are simply asking for a maximum of efficiency». [1] [Page 6. 6].
7a. «Zitterbewegung» (the instantaneous movement of a particle), for example, because of participation in such vibrations two projects, without the speed limit of light, although the full the average motion of a particle is characterized by a velocity less than the speed of light. Therefore for the projection center — of a particle, the locality principle does not break. The locality for all particles is that space is three-dimensional and have a Euclidean definition of distance. «Locality. All configurations one needs to know to determine the behavior of an object at a given spot must be lying in its vicinity. This means that we will have to define distances. Only points at very small distances from a given point are relevant for what happens there. What ‘vicinity’ really means still has to define»[1] [Page 6. 14].
8. After going through the steps of Verlinde, considering the thermodynamics of the holographic screen, we conclude that the acceleration is associated with the entropy gradient. This is our one of the basic principles: inertia is a consequence of the fact that the resting particle will continue to rest, since it is not subjected to the action of entropy gradients. The principle of equivalence leads us to the conclusion that this is the very law of inertia — the rule that stems from entropy.
«Velocity. Any object for which it has been decided how it behaves when at rest, will behave very similarly when it moves along a straight line in any direction, with any constant velocity (within limits, see the next rule). The rule of its behavior at this velocity must be derivable in a simple way from what the rules are when it stands still. [1] [Page 6. 30].
To improve visualization of the quantum simulator «IsAN», three generations of particles are identified by three spectra: green, blue and red. In the grand unification theory, particles: quarks (u, d) and leptons are grouped into three generations: quarks (u, d) with an electron (e -) and an electron neutrino (ν_e) form the first generation, quarks (c, s) c muon (μ -) and muonic neutrinos (ν_μ) form the second generation, and the quarks (t, b) together with the tau lepton (τ -) and the tau lepton neutrino (ν_τ) are the third generation:



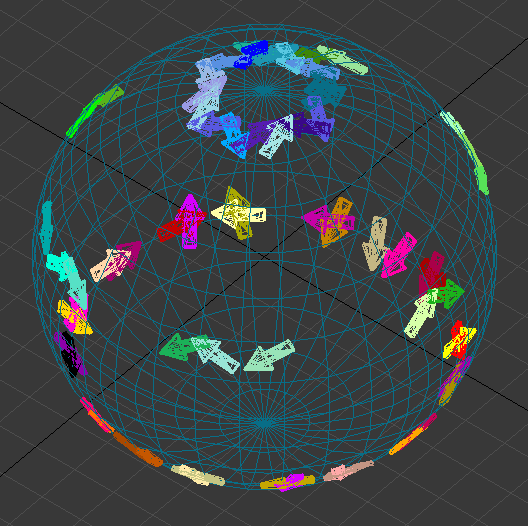



Reproducing realistic quantum models for locally interacting quantum particles along the lines proposed.
The space-time arises as an emergent phenomenon of the quantum degrees of freedom or pairwise exchanges of projections (Is-Is¹ or AN-AN¹) that are entangled and live on the holographic horizon 2D of the decoherence of quantum processes According to some prominent researchers in emergent gravity (such as Mark Van Raamsdonk) spacetime is built up of quantum entanglement.[27] This implies that quantum entanglement of projections is the fundamental property that gives rise to space-time (emerged 3D).
The anisotropy of the Universe

Thermodynamics on a holographic surface, it is a result of the decoherence of quantum processes.
Commensurate in scale with the Holographic Principle was the discovery of the anisotropy of the Universe in 1992 (anisotropy of cosmic microwave background (CMB) — (this the difference of temperature in different directions on the sky) [5] Experimentally confirmed by the anisotropy of the CMB and the discovery of coherent acoustic waves in the early Universe is of great importance not only for cosmology but for the whole of natural science as a whole. It can be said that large-scale three-dimensional sound coherent oscillations act before recombination period and ended after 379,000 years, but did not disappear completely, and recorded big scale on the sky. As a result, the temperature anisotropy of the Universe, according to the Holographic Principle, may be projected on its holographic screen. It is experimentally confirmed the fact that coherent oscillation of the elements of mass can be projected without any loss of information to the specific locations of the holographic screen. All calculations and experimental data in the modern cosmological model, in particular, explain the observed anisotropy of the Universe are connected with the speed of sound three-dimensional coherent oscillations of the primary plasma. the discovery of CMB confirmed the theory of the hot Universe and is now one of the most important facts supporting the theory of the Big Bang and the expanding Universe. We can say that experimentally is not confirmed equipartition of temperature on the cosmological horizon of the inflationary Universe. Investigating thermodynamics on the holographic screen, we must take into account the impact of it’s of global temperature anisotropy on the dynamics of the projections of phenomena. The dominance of gravity, on a large scale, in particular, and existence all four known forces a whole can be explained by the influence of a large-scale thermal anisotropy Universe [5],[39].

The CMB dipole anisotropy. The color scale shows a spread of ±3.5 mK.
For experimental verification of the Holographic Principle is offered unusual gyroscope MGGF. It is assumed that MGGF can generate and control the direction of AFG, can be used as a propulsion system and can easily be reprogrammed to work as a device for measuring the geometry and dynamics of the Universe in the real-time (without limiting the speed of light). Let us consider in detail how it works.
To demonstrate the possibilities of generating AFG we define that is very important: Although the bits of information are encoded on a two-dimensional (2D) screen the observed images appear three-dimensional (3D) since their nature is holographic.
«Usually, holography is studied in relativistic contexts. However, the gravitational force is also present in our daily non-relativistic world» [25] [page 3. 5].
«we will argue that the central notion needed to derive gravity is information» [25] [page 2. 23].
The relationship between entropy and information is that the change in information ΔI is represented by a negative change in the entropy ΔS.
ΔI = — ΔS.
On the other hand, gradients of temperature, entropy, and force are associated with acceleration and the resulting mass:
«We can express the entropy change in terms of the acceleration» [25] [page 11. 14]. «Thus, we conclude that acceleration is related to an entropy gradient. This will be one of our main principles». [25] [page 11. 22].
ΔS ∼ α
To shorten the text, we mean that the temperature, entropy, and entropic forces are on the holographic screen — the cosmological horizon of the Universe.
Let’s start with the postulate of the Holographic Principle:
1. «In the limit of a very large region, the bonding surface can be taken to be a flat plane at infinity. In some way, the phenomena taking place in three-dimensional space can be projected onto a distant «viewing screen» with no loss of information» [3] [page. 3. 18]. This means that all the information, the receiver, the transmitter, and the observer is on the holographic surface the cosmological horizon of the Universe. For us, it is very important not to forget and this greatly simplifies the exchange and processing of information for the observer.
2. Unusual gyroscope MGGF is that the cycle of its spherical rotor makes one complete revolution around the three axes. The movement of the rotor in a vacuum is controlled by a computer control system.
3. Since the spherical motion (forced coherent oscillations) of the spherical rotor is made around the three orthogonal axes, then there we have are six areas (groups) of angular accelerations elements of mass. All elements mass of the rotor moves over the surfaces of concentric spheres around a fixed point — the center of mass. Nodes and anti-nodes of angular accelerations create a stationary interference pattern. Thus, we are dealing with the cooperative a quantum phenomenon (we artificially create an ensemble of particles).
4. According to the Holographic Principle, we can make this projection the six groups of angular accelerations (αCi) elements of mass (gradient entropy) on a holographic screen — the cosmological horizon of the Universe without losing information. Actually, the projection and is not required, if you understand the essence of the Holographic Principle. In the presence of horizons, it is natural to define on the horizon global gradient temperature ΔTgl.
5. We have the stationary interference pattern of the six groups of angular accelerations (gradient entropy) is on diametrical sections of the holographic screen. rotor control system produces shifts of the rotor (any the pairs (4 of 6) projections, reverses the rotation of the half-line). Gradients entropy of αEi — angular accelerations (they emerge at displacement elements of mass) by moving on the screen part of the projections are experiencing the different entropic force as they interact with a certain dipole global gradient temperature. Thus we are able to control the position of the on-screen projections of two angular accelerations αCi and αEi. The center of projections angular accelerations is displaced under the action of the forces of entropy associated with a temperature gradient. therefore, the center of accelerations of the rotor is attached to the entropic force «F» — this is a long-range gravitational force.
6. Let us consider.
The thermodynamics on the holographic screen (hs) with the dimension of «2 + 1» (2D).
For 3D. Considering that the entropy of a system depends on the distance ∆x, an entropic force Fentr could arise from the thermodynamical conjugate of the distance as [25] [page 7. (3.7)]
Fentr ∆x=T∆S (1)
To give an explanation of the force acting on particles, E. Verlinde determined the work that is done at the expense of this force and showed that it can be naturally represented as a change in entropy multiplied by constant temperature (1). The difference with respect to the case for the pair of particle projections is that the screen temperature is not constant and the system is in a state of quantum coherence. Indeed, in the general case, the situation is not equilibrium. The information on the screen is represented by temperature and entropy gradients.

The gradient operation transforms the 3D hill (left), viewed from above, into the vectors flat field 2D (right) on the holographic screen of the Universe. It can be seen that the direction vectors «in the hill» and the longer the vector, the steeper the slope. The projection of the gradient is always perpendicular to the surfaces of the level lines on the holographic screen. The exception is singular points of a plane field in which the gradient is zero.
dT/Δx,dT/Δy,dT/Δz=ΔTi
(2)
ΔT — positive or negative temperature difference at two points per unit distance between them a vector quantity dT/ΔX,dT/ΔY=ΔT (3)
we obtain:
Fentr =ΔT∆S (4)
where Fentr on 2D of the screen, «ΔT» — gradient temperature , «ΔS» — gradient entropy caused by the acceleration either projections of the matter.
For 3D. The product Fentr Δx can be considered as the energy that should be applied to the system in order to withdraw it from the equilibrium state. The existence of a vector factor Δx (perpendicular to the screen) is the reason that the world seems to us to be three-dimensional. Space occurs on a macroscopic level only after discretization. Consequently, with each configuration of matter, the final entropy is connected. This entropy measures the microscopic amount of information that is invisible to a macroscopic observer. In general, this amount of information will depend on the distribution of matter. This information will be processed by entering the microscopic evolution of the screen, which seems random from a macroscopic point of view. Such an assumption goes back to Bekenstein’s thought experiment in the derivation of his famous equation for entropy. He considered a particle with a mass m that approaches the horizon of a black hole. Directly near the horizon, the particle merges with it. As a consequence of the infinite redshift, the mass of the particle increases the mass and area of the horizon by some small (classical) value. As soon as the particle is at a distance of the Compton wavelength Δx from the horizon, it can be regarded as part of a black hole. Then it increases the mass and area of the black hole horizon by a small amount that Beckenstein associated with one bit of information, which led him to the law of correspondence between the area of the black hole’s horizon and its entropy.
For 3D. Verlinde considered the situation, not alongside a black hole, but with a flat non-relativistic space, ie, next to a small plate — a holographic screen, and a particle of mass m that approaches it. Eventually, the microscopic degrees of freedom of the particle merge with the screen, but just before that, some amount of information is transmitted to the screen. Thus, a holographic direction appears perpendicular to the screen. Guided by Bekenstein’s considerations, Verlinde wrote down the equation for the entropy increment associated with the mass [25] [page 4] (3.6):
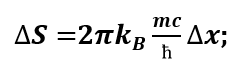 (5)
(5)
Where c is the speed of light in a vacuum, ħ is the Planck constant.
How does the entropic force arise?
Each cell of the screen by definition contains one bit. Assuming the fulfillment of the Holographic Principle, let us write down that the information capacity of a spherical screen is proportional to the area of the shell:

(6)
Where N is the pair of entangled bits.
In our closed system, the energy E is equivalent to the mass of the physical body M, which is concentrated in the part of the space surrounded by the screen. Since temperature and acceleration are closely related and have a direction in a three-dimensional space perpendicular to the screen, then, in accordance with the Holographic Principle, we can project them without loss of information. Unruh showed that the observer in the accelerated reference system has a temperature T:

(7)
Where α is the acceleration, kB is the Boltzmann constant. As will be shown below, using this equation, we can display the temperature associated with the bits on the screen.
According to the proposed method of projecting the phenomena on the screen, suggested by L. Susskind [3], the memory cells of the screen with the temperature projected on it, connected with the physical body, occupy one hemisphere of the screen, this is what we call the global temperature gradient.

We have chosen the usual position of the center of mass of the physical body when it is displaced relative to the center of the screen. According to the proposed method of projecting the phenomena on the screen, suggested by L. Susskind, the memory cells of the screen with the temperature projected on it, connected with the physical body, occupy one hemisphere of the screen, this is what we call the global temperature gradient. Nevertheless, the energy equivalent to matter and uniformly distributed across the cells of the screen must, subject to the Holographic Principle, carry information about the mass and coordinates of the physical body in three-dimensional space without loss. Note that these conditions are contradictory. In the classical approximation, the total energy that is associated with the physical body cannot be uniformly distributed across the screen, otherwise, information about its coordinates will be lost. To solve this problem, it is required to break up the total energy equal to the mass of the physical body into kinetic and potential and, only then it can be assumed that the total energy tends to be uniformly distributed among the memory cells. Thus, we come to the important conclusion that, for any physical body, there is its own global temperature gradient on the half of the screen, which carries information about its mass and coordinates (potential energy), and the displacement of the global temperature gradient under the action of entropy gradient displacements (Kinetic Energy) complements the associated energy E to the full. Then we can assume that the entropic force arises from the movement of the global temperature gradient on the inflation screen, which leads to a shift in the center of the projections of the accelerations of the mass elements or the coordinates of the physical body in the three-dimensional space. In full accordance with the conclusions of Verlinde, the emerging entropic force in the three-dimensional space acquires the appearance of a gravitational force.
Obeying the Holographic Principle, complete information about the physical body and its coordinates, related to the kinetic and potential energy, tends to spread evenly across the screen. This means that any physical body has inexhaustible energy from the source of kinetic energy necessary to move its global temperature gradient across the screen. Kinetic energy is the result of inflation — the accelerated expansion of the screen itself (the continuation of the Big Bang).
If our assumptions are correct, then thermodynamics on the surface of the screen must inevitably lead to the conclusion of fundamental laws, in particular, to the Law of World Gravitation. Let’s consider more in detail
So, we assert that the potential plus kinetic energy on the screen is equal to the total energy (Ek + Ep = E). Then the total energy equal to the mass of the physical body tends to be evenly distributed between bits of the screen N (by ½kBT for each bit).
![]()
(8)
Where kBT is the temperature of one cell. We use the well-known equation for energy.
![]()
(9)
Where M is the mass of a physical body enclosed in a part of the space bounded by a spherical screen. The surface area of the spherical screen is A.
![]()
(10)
Where R is the radius of the screen.
If we now introduce a second physical body of mass m into consideration, the position of the global temperature gradient on the screen will cease to be the same. In the general case, the temperature gradients will no longer be given by the same rule.
In quantum mechanics, there is that radical idea that particles do not just move along the shortest path, but go all the way possible routes pass, including random zigzag wanderings. From the position of the Holographic Principle, this process extends over the entire surface of the holographic screen of the Universe with a global temperature gradient on it. The quantum/holographic mechanism of moving, now the projections of particles of physical bodies around the screen and their interaction with temperature gradients is the source of the entropic force applied to the center of the projections. This is a key postulate for explaining the mechanism of mass generation and entropic force (gravitational force). Each projection of a particle of a physical body has traveled both in the present and in the future, passing through all possible angular movements. The contribution from all angular movements stories, except for one single, classical, was reduced. Thus, the existence of the Hamiltonian principle in classical physics is a consequence of the displacement of projections of particles along the screen and their interaction with the global dipole temperature gradient of the Universe.
Inflation of screen adds to the gravitational interaction an additional repulsive force between the masses, a kind of anti-gravity that reflects on the gravitational constant G. Therefore, in the equation for the entropic force, it is necessary to introduce a constant G, which can be equal to Newton’s gravitational constant for our Universe.

Projections of global temperature gradients of two bodies on the holographic screen of the Universe.
The entropic forces tend to a minimum the distance R between two bodies. This process occurs because when we introduce a second body into the system, the balance between kinetic and potential energy for each of the two bodies is violated. Accordingly, the balance of the opposing forces moving the projections of particles on the screen, connected with the bodies M and m, and the force of the screen creating inflation, are violated. Projections of particles M and m when moving them along the screen interact with temperature gradients m (circle) and M (ring). As a result of the imbalance, the forces of expansion of the screen entropy increase, which increase the area of the screen with temperature gradients m (circle) and M (ring), form, respectively, more than M. For the body of a larger mass M and, accordingly, the disbalance of entropic forces and, consequently, the body m approaches M with a large acceleration, which is interpreted in 3D as a result of the action of gravity. The distance R rapidly decreases, and with it the centers of the projections also move rapidly. Eventually, the temperature gradients merge, and, therefore, the bodies collide. In this situation, for two black holes with the maximum information density on the inflation screen, they merge, and the displacement of the particle projections associated with them is identified with «radiation» and leads to a known «evaporation.» Thus, the information is preserved, and black holes are interpreted in 3D only as 2D objects. We conclude that the natural identification of gradient of temperature and information density on the inflationary holographic screen direct substitute the expression for the number of bits N (6) that determine the temperature T (7). To determine the force in (4) we use the expression for entropy change (5), finally substitute (10) and G, we get:
![]()
(11)
Thus, the force of gravitational interaction of two bodies arises as a result of a holographic scenario, which explains its long-range action.
We use equation (4) and replace the temperature by (7), the entropy gradient by (5) and obtain the second Newton law.
![]()
(12)
Since each bit carries an energy of 1/2 kBT, then their number N is determined from the relation:
![]()
(13)
When we substitute this equation in (5) and use (7), we can express the entropy increments through acceleration:

(14)
Combining equations (4), (14) and (13), expressing the temperature through the mass, and the entropy gradient through acceleration, we again arrive at the equation F = mα for the entropic force. However, by entering the number of bits associated with the energy on the screen, we demonstrate that the constant c and ħ fall out of the ratio, which corresponds to expectations. This conclusion means a lot to us, for example, that the entropy (gravitational force) can be artificially created with the help of a hybrid of a classical and quantum device for generating accelerations (an unusual gyroscope) without using exotic masses and energies. The kinetic energy of accelerated screen expansion associated with the mass of the rotor of an unusual gyroscope can be used in the recovery mode and used as an inexhaustible source of clean energy.
Newton’s Second Law for the mass of particles (12), from the laws of thermodynamics on the surface (on the holographic screen).
F∼m. (15)
F — entropic force, m — the mass of a particle. (We have a constant rotational acceleration of the projections of particles since the oscillations are coherent).
Then, the gravitational force obtained in the classical system (as a multi-particle quantum phenomenon) is equal to:
Fgrav=ηmα² (16)
where Fgrav — gravitational force. The emergent laws of gravity contain gravitational force describing the ‘elastic’ response due to the entropy displacement of the projection.
η is the order parameter (1> η> 0) (the inverse value characterizing the influence of the external environment on the thermodynamic system (including the gravitational influence)).
α² = αCiαEi / 6 gravitational acceleration (when αCi = αEi). 6 — the number of projections of acceleration groups on the holographic screen.
αCi — coherent acceleration (acceleration resulting from coherent oscillations).
αEi — is a jerk (the first derivative of the coherent acceleration resulting from mass shifts around the center of acceleration).
This means that to obtain long-range gravitational forces do not require exotic masses and energies.
Holographic Principle concludes that: gravity is explained as an entropic force. The equivalence principle leads us to conclude that it is actually this law of inertia whose origin entropic. This thermodynamics on 2D, arising from the statistical behavior of microscopic degrees of freedom associated with a global temperature anisotropy and localized on the holographic screen of the Universe. Thus the force of gravity and his long-range is not postulated but derived from a holographic scenario.
In contrast to the entropy change when a particle approaches the screen equidistribution temperature, the entropy change when each of the projections of particles (elements of mass) moving on the screen interacts with the gradient of temperature and carries more information than when artificially introduced the equipartition of temperature on screen. As a result of the interaction of the gradient of the entropy projections particle arising entropic force applied to the geometric center of the particle. Therefore, this mechanism is maybe responsible for the appearance of a mass. A result of the encoding information on the holographic screen appears mass/energy, gravity, and space-time itself. Unusual gyroscope with six degrees of freedom MGGF can be used for a detailed study of this assumption.
The series generated in MGGF directed long-range gravitational forces leads us to be able to control gravity.
MGGF device can answer the question: Does the Holographic Principle is valid, according to which the physics of our 3D n-dimensional space-time is equivalent to the physics of the hypersurface with the dimension of 2D. In addition, we get the information directly from the surface of the cosmological horizon in real time and without limiting the speed of light
Gravity — ordered action entropic forces on the projection of the phenomena on a 2D the holographic screen. As a result, the centers of the projections are changing their position in 3D. Entropic (gravity) force — is the result of the interaction of the entropy gradient on the holographic screen caused by the acceleration of matter and the global temperature gradient, known as anisotropy of the Universe. Thus, the movement of information on the 2D holographic screen leads to the long-range directional gravity force in 3D.
After transformation in 3D away quite easily possible to deduce the fundamental laws of Newton (in particular the Second Law). This means that to obtain long-range gravitational forces do not require exotic masses and energy (see below Formalism Verlinde in the emerging space-time (the physics of 3D on the border of 2D).
Newton’s third law is not violated since the size of a closed system is increased to the cosmological horizon of the Universe. Series directed long-range gravity forces leads us to manipulate gravity. Note that the computer of the rotor spherical motion control system has received information on the situation of the global dipole temperature anisotropy of the Universe without limiting the speed of light.
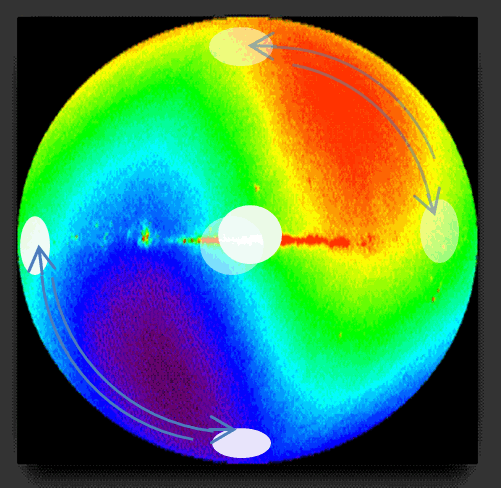
Global temperature gradient Universe and projection on a holographic screen interference pattern of the six groups of angular accelerations αCi (respectively, gradients of entropy). We can see spatially periodic structure six of equidistant spots. Arrows indicate the possible direction of the angular acceleration displacement αEi.
Where F_grav is the gravitational force, y is the order parameter, the value lying between zero and unity, m is the mass of the rotor of the unusual gyroscope, and a is the product of two equal accelerations. One of which is the rotational acceleration caused by artificial coherent oscillations of the rotor and, second, is caused by a controlled displacement (one of 60 variants).
Obtaining a directed gravitational force in an unusual gyroscope does not contradict the law of conservation of momentum since the size of a closed system is the holographic screen of the Universe.
If our assumptions are correct, then the prospects are opened with the use of an unusual gyro MGGF for:
- Artificially creating coherent vibrations of the rotor of an unusual gyro, controlling the direction of the acceleration of the elements of mass, we can create entropy (gravitational) forces on the screen in any chosen direction and, therefore, control gravity.
2. Generating AFG and determining its direction, we can build a hybrid of the classical and quantum device for measuring the parameters of the Universe in real time.
MGGF
1. Base.
2. Enclosure.
3. The Stator (diameter front section).
4. Frame.
5. Rotor.
6. Magnets.
7. Magnetic point (one of the magnets, as an exception, is not displaced).
8. Vacuum cavity (diameter front section).
9. Solenoids.
10. Sensors optical.
11. Slave controllers and drivers of induced coils.
12. Computer.
13. Accumulators.
14. Solar batteries.
15. Retaining bolts.
Let us discuss the concept of the MGGF design, ‘a thick-walled sphere with the magnets in a vacuum inside another sphere with induced coils’. The design allows for three-dimensional oscillations of the balanced ceramic rotor 5 (hereinafter, the rotor) with the magnets pressed into it around its center of mass. Such gyroscope without mechanical axes can be obtained by a master electromagnetic suspension that acts based on the principle of the rotor active levitation with magnets in the magnetic field. The rotor displacement from a predetermined equilibrium position is measured by the position sensors. The signals from the sensors are processed by a multi-core microprocessor control system which regulates the currents pulse in the induced windings of the stator so that the magnetic forces return the rotor to the predetermined position and can simultaneously produce full angular rotations of the rotor in any direction under computer control. The control program is provided with the possibility of stabilizing the cyclic rotor speed.
Force coherent fluctuations of a rotor to make angular accelerations (αCi) of each element of mass. On multiple concentric spherical surfaces, angular accelerations take constant positions in space, in a time of a cycle and create an interferential system.
In full accordance with the Holographic Principle, one of the most important properties of coherent fluctuation of a rotor is to concentrate the gradients entropy displacement by its angular accelerations round each of semiaxis of motionless Cartesian coordinates on a «remote» holographic surface of the Universe and angular accelerations may be projected with no loss of information and travel on it without time delay.
Further, we will discuss the holographic dynamics as applied to the spherical rotor in a vacuum. Such a closed dynamic system, as we will see below, has central and translational symmetry. It will include (along with the rotor and stator) concentric spherical holographic screens with the entropy associated with the local space occupied by the rotor, its local temperature, and its dynamics.
Let us start with the definition of coherent oscillation of a classical body.
“The motion of a physical body when only one its point О remains fixed all the time is called the rigid body motion (rotation) around a fixed point О. In this case, all points of the physical body move along the surface of concentric spheres, the centers of which are located in the point О. Therefore, such motion is called the spherical motion of the body. Based on the definition of the spherical motion, we obtain parametric equations of the coherent oscillation of the elements of mass ”.
“Forced coherent oscillations of mass elements are created by spherical motion of a physical body and are performed by angular displacements of its points, at the intersection of the axes of fixed Cartesian coordinates, with surfaces of concentric spheres according to the laws of sine and / or cosine for equal and small time intervals, triads”.
(θx= Cosθ
(θy=-Sinθ
(θz= Sinθ
θx, θy, θz — sequential angular displacement of any previously selected points on two meridians and the equator of the spherical rotor’s, around orthogonal to their flatness the corresponding fixed Cartesian axes associated with the accelerated observer. Parameters: θ = πt and -1 ≤ t ≤ 1; where θ is the geometric angle defined by an arbitrary direction in a clockwise and /or counterclockwise direction, starting with the corresponding semiaxis, and t specifies the required accuracy of the angular displacement. When Δt → 0 are the coordinates of the center and ε → 0
We have an extremely simple equation of the rotor spherical motion of an unusual gyroscope in three-dimensional space. Only eight main directions.
The coherent fluctuations of the rotor occur in a vacuum. Such thermodynamic isolation of the rotor from the nearest external environment is crucial because it eliminates the possible influence of the temperature and entropy changes on the rotor surface. Thus, in a vacuum, the rotor acquires local temperature and entropy when matter (particles) is displaced.
Moreover, such rotor oscillations are characterized by central and translational symmetry, along with mutual orthogonality, as they occur around each of the axis (x¡).

The Graph shows six zero — angular speeds of revolutions of the rotor, when the rotary acceleration (αС) becomes zero, for each of the Cartesian coordinate semiaxes.
αС (x+), αС (x-) — accelerating along the X-axis, αС (y+), αС (y-) — Y-axis, αС (z+), αС (z-) — Z-axis.
It is important to note that, according to the above equation (10), the arising acceleration (αСi) of all points – the electrons, protons (we will treat them as rigidly bound point particles in the atoms, as the elements of the rotor mass) is distributed in space and in cycle time. The phases of the oscillations around each of the axes are a shift in cycle time to 90° and, therefore, are distributed in space and in cycle time; see Figure 1. The harmonic functions of the angular movement of the points (the rotor mass elements) are periodic relative to both time t, and to the (x¡). Thus, equipartition of the extremes of harmonic functions of speed (when αСi > 0) in cycle time and in space leads the dynamic system isolated from the external environment to the spatial and temporal coherence.
Relying on the above discussion, let us define the scale gravitational force. Due to the gyroscope property to acquire stability in an effort to save its determined direction relative to the world space and as a result of the rigid connection between all material points (the electrons) of the rotor, they all get the rotary acceleration (αCi).
It doesn’t have an outside or an inside. It just has a rubber surface. You have to learn to think of the surface of the balloon as being all there is. It’s all there is». L. Susskind.
The projections acceleration the surface are possible because: «… have determined that, to high precision, space in our cosmos is flat» [5] [page 1371].

Red and purple are conditionally shown temperature gradients Tu — dipole lobes (on the surface anisotropy) [5]. For a case of coherent fluctuation of a rotor the entropy gradients associated with its angular accelerations: αCX+ =0, αCX-=0, αCY+ =0, αCY- =0, αCZ+ =0, αCZ- =0 concentrate around motionless semiaxis (x¡) on surface of (fig. at the left). For a rotation case (incoherent fluctuation) of a rotor around the main axis, gradients of entropy are making displacement on all surface of (fig. on the right). On two spheres by white color, the arrangement of gradients of entropy on a surface is conditionally shown. For the generation of the directed gravitational force, the program of management of the coherent fluctuation of a rotor makes the displacement of its points round two of three axes of motionless Cartesian coordinates. This results in the acceleration of displacement (αEi). Options are presented in Tab. A, B, C, and D
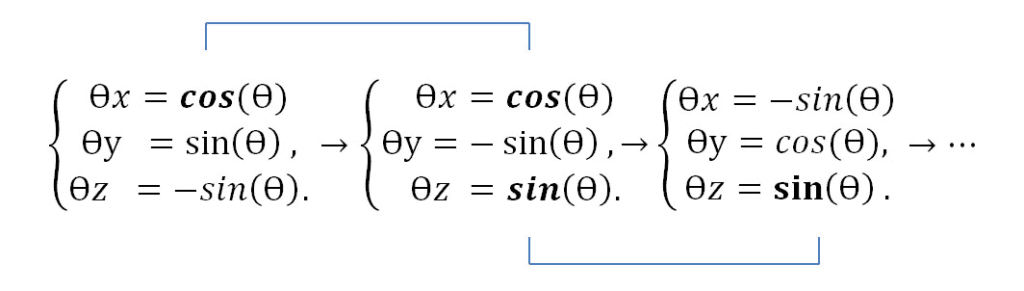
Artificial short-term decoherence
Artificial short-term decoherence in unusual gyroscope — a violation of coherence — is the disappearance of coherent properties, associated with the loss of constancy of the relative phase between sources, which, for example, leads to the destruction of the interference pattern from accelerations, which we discussed above.
In cooperative quantum phenomenon — decoherence is the interaction of a quantum system with the environment, in which the quantum state of the system changes. From the point of view of the theory of quantum information of decoherence, there corresponds the emergence of entanglement between the degrees of freedom of the quantum state and the degrees of freedom of the environment.
The scaling and directed gravitational force can be artificially obtained by displacement the position of coherent fluctuations matter relative to two of the three fixed Cartesian coordinate axes, which causes changes in the local entropy on the holographic screen. This can be regarded as a cooperative quantum phenomenon. Thus, the directed scale gravitational force can be generated during the reverse transition of the system to more probable (realized by the greater number of microstates) macro state at the moment of the translational symmetry violation. The fixation of the occurrence of gravitational force can be carried out on a torsion balance. Torsion balance is a compact instrument for measuring the gravitational force and verifying the cooperative quantum effect in unusual gyroscope MGGF based on an elaborately designed Cavendish balance. It uses a reflected laser beam.
Experiment 2.
Repulsion of a copper and wooden frame near a rapidly rotating aluminum disk (7000 rpm) in a vacuum. (Prof. V. N. Samokhvalov). Non-contact interaction in a vacuum (chamber pressure 2×10¯³ mmHg). This experiment with non-magnetic materials, a visual demonstration of acting at a distance of entropic forces in a vacuum [24].
The effects are only in a vacuum, independent of the electrical properties of materials of the disk and not involve the emergence of electric and magnetic fields.
——————————————————————————————————————————————
Optimizing Acceleration Performance for Rotor with Large Vacuum Clearances.
Annotation.
This article presents the design of an unusual gyroscope (hereinafter referred to as an engine), which gives the minimum acceleration time for different ranges and directions of speeds of a spherical rotor with magnets inside the evacuated spherical cavity of the stator. A three-dimensional synchronous machine is used to create three-dimensional coherent oscillations of a spherical rotor in magnetic levitation and with a large vacuum gap.
Keywords — acceleration, large evacuated gaps, magnetic levitation,
permanent magnets, synchronous machines.
An ELECTRIC MOTOR with a large vacuum gap, a high-purity for the isolated thermodynamic system, can only be guaranteed only by the absence, avoiding all sources that generate vibrations, including mechanical bearings. Therefore, for these applications, it is advantageous to use motors with magnetic levitation and a large vacuum gap. Creating the possibility of accelerating of rotor such engines is crucial since they are constantly being operated in the mode of changing the direction of the moving. Here, the resulting acceleration time determines the performance of the equipment and, ultimately, the cost-benefit ratio. Therefore, the complexity of the design of the engine is to maximize the accelerating ability of the engine with a large vacuum gap, which allows you to insert the wall of the separation chamber between the rotor and the stator. Although several publications on large-air-gap motors exist [1]–[4], they do not explicitly treat the parameters and geometry optimization for maximum acceleration resulting from three-dimensional coherent oscillations of a rotor.
The prototype system used as an example in this paper has a mechanical vacuum gap of 7 mm, which is a good representation of a large vacuum gap. Magnetic bearing offers some major advantages that are crucial for the application. The advantages are an almost unlimited lifetime, adjustable bearing parameters allowing for an active unbalance compensation (consequently avoiding processor-time costly eccentricity detection methods presented in [8] and [9]). Furthermore, due to the built-in fault diagnostics of the magnetic bearing [10], costly motor failure detection is absent.
A simplified schematic view of the prototype system is shown in Fig. 1.
See more: https://isan.com.ua/articles
———————————————————————————————————————
«What exactly is an Entropy telescope?» — is a hypothetical device that operates based on measuring entropy forces applied to the center of mass of the rotor of a Gyro-6DoF gyroscope with a coherently oscillating rotor and unique holographic properties. The device works by taking a solid spherical rotor with magnets and rotating it around three axes in a vacuum chamber for one cycle using electromagnets. This is accomplished by angularly displacing the points of the rotor on the equator and two meridians during one cycle according to sine and/or cosine laws with a constant frequency and phase. As a result, there are six stationary groups of an interference pattern of the accelerations of points on the diametrically located areas of the spherical rotor.
The idea is that if the holographic principle is a physical model, not a mathematical one, then we can not only project these acceleration groups onto the holographic horizon without losing information but also move them across the screen by interchanging two of the three axes of rotation of the rotor. As a result of moving four of the six groups of accelerations of the interference pattern, there will be interaction with the temperature gradients of the screen, and an entropy force will be applied to the center of mass of the rotor, which we can measure. Thus, by scanning the holographic horizon, we will obtain information directly from its surface, which makes it possible to look deeper into the universe beyond the cosmological horizon.
AI: » The entropy telescope may be of interest to physicists, astrophysicists, and cosmologists who study the cosmic structure and characteristics of the Universe. It may also be of interest to engineers involved in the development of new technologies for measuring and processing information. The coherently oscillating rotor gyroscope prototype could be useful for developing new optical interferometry techniques and navigation systems, as well as for applications in spacecraft and other engineering projects where accurate measurement of acceleration and attitude is required.»
References
[1] G. ’t Hooft, «Fast Vacuum Fluctuations and the Emergence of Quntum Mechanics» https://link.springer.com/article/10.1007/s10701-021-00464-7?utm_source=facebook&utm_medium=social&utm_content=ads&utm_campaign=SPSN_2_RC01_PS_JNL_foPhyGtHooft&fbclid=IwAR0heqVGU8gV60vch5HpaRyOdBdIbayLusWo2V8Wj4IGy4fb5XDD4SHcbbk
[2] G. ’t Hooft, “Dimensional reduction in quantum gravity” (1993) [arXiv:gr-qc/9310026].
[3] L. Susskind, «The World as a Hologram». J. Math. Phys. 36 (1995) 6377, arXiv:hep-th/9409089.
[4] H. Casini, M. Huerta, J. Hung, A. Sinha, M. Smolkin & A. Yale. «Holographic Entanglmarkent Entropy».
[5] George F. Smoot «Cosmic microwave background radiation anisotropies: Their discovery and utilization» REVIEWS OF MODERN PHYSICS, VOLUME 79, OCTOBER–DECEMBER 2007.
[6] J. Raphael Bousso «The Holographic Principle» http://arxiv.org/abs/hep-th/0203101.
[7] J. D. Bekenstein, “Black holes and entropy,” Phys. Rev. D 7, 2333 (1973).
[8] G. ’t Hooft » The Cellular Automaton Interpretation of Quantum Mechanics» 2014 https://arxiv.org/abs/1405.1548
[9]P. C. W. Davies, ”Scalar particle production in Schwarzschild and Rindler metrics,” J. Phys. A 8, 609 (1975)
[10] W. G. Unruh, «Notes on black hole evaporation» Phys. Rev. D 14, 870 (1976).
[11] A. L. Dmitriev, E. M. Nikushchenko, S. A. Bulgakova «NONZERO RESULT OF MEASUREMENT OF ACCELERATION OF FREE FALLING GYROSCOPE WITH THE HORIZONTAL AXIS» http://arxiv.org/ftp/arxiv/papers/0907/0907.2790.pdf
[12] Aitor Lewkowycz, Juan Maldacena «Generalized gravitational entropy» http://arxiv.org/pdf/1304.4926v2.pdf
[13] E. Santos, Bell’s their mark and the experiments: Increasing vampirical support to local realism: quant-ph/0410193, Studies In History and Philosophy of Modern Physics, 36, 544-565 (2005).
[14] Zurek W. H. «Decoherence, in selection, and the quantum origins of the classical», Rev. Mod. Phys. 75, 715 (2003).
[15] Tittel, 1998: W. Tittel et al., Experimental darkons ration of quantum correlations over more than 10 kilometers, Physical Review A 57, 3229.
[16] Shinsei Ryu, Tadashi Takayanagi «Aspects of Holographic Entanglmarkent Entropy».
[17] David Bohm: Wholeness and the Implicate Order, Routledge, 1980 (ISBN 0-203-99515-5).
[18] M. Milgrom, «MOND — Particularly as Modified Inertia», arXiv:1111.1611
[19] Dennis Dieks, Jeroen van Dongen and Sebastian de Haro «Emergence in Holographic Scenarios for Gravity»
[20] Misra B., Sudarshan E.C.G «The Zeno`s paradox in quantum theory».
[21] Tadashi Takayanagi «Entanglmarkent Entropy and AdS/CFT».
[22] Daniel Asenjo, Fabien Paillusson, and Daan Frenkel «Numerical Calculation of Granular Entropy» Phys. Rev. Lett. 112, 098002 – Published 5 March 2014.
[23] Frank Wilczek. «Superfluidity and Space-Time Translation Symmetry Breaking» Phys. Rev. Lett. 111, 250402 – Published 18 Declarer 2013.
[24] (V. N. Samokhvalov “Non-electromagnetic Force Interaction in Presence of Rotating Mass in Vacuum,” [International Journal of Unconventional Science] 1(1), pp. 6-19, 2013 (Article received: 18 Nov 2012; Article accepted for publication: 23 Apr 2013) http://www.unconv-science.org/en/n1/samokhvalov/
[25] [Verlinde, 2010] Erik Verlinde. «On the Origin of Gravity and the Laws of Newton». arXiv:1001.0785v1 [hep-th].
[26] L. Bolotin1, V.V. Yanovsky «HOLOGRAPHIC DYNAMICS». http://fs
[27] Van Raamsdonk, Mark (19 June 2010). «Building up spacetime with quantum entanglement». General Relativity and Gravitation. 42 (10): 2323–2329. arXiv:1005.3035. Bibcode:2010GReGr..42.2323V. doi:10.1007/s10714-010-1034-0.
[28] Yi Wang «Towards a Holographic Description of Inflation and Generation of Fluctuations from Thermodynamics» arXiv:1001.4786v2 [hep-th] 31 Jan 2010
[29] [Verlinde, 2016] Erik Verlinde. «Emergent Gravity and the Dark Universe» https://arxiv.org/pdf/1611.02269v1.pdf
[30] Margot M. Brouwer, Manus R. Visser, Andrej Dvornik, Henk Hoekstra, Konrad Kuijken, Edwin A. Valentijn, Maciej Bilicki, Chris Blake, Sarah Brough, Hugo Buddelmeijer, Thomas Erben,Catherine Heymans, Hendrik Hildebrandt, Benne W. Holwerda, Andrew M. Hopkins, Dominik Klaus, Jochen Liske, Jon Loveday, John McFarland, Reiko Nakajima, Cristóbal Sifón,Edward N. Taylor » «First test of Verlinde’s theory of Emergent Gravity using Weak Gravitational Lensing measurements» https://arxiv.org/abs/1612.03034
[31] Yun Soo Myung, Hyung Won Lee, and Yong-Wan Kim «Entropic force versus temperature force» https://arxiv.org/abs/1006.1922v1
[32] Niayesh Afshordi, Claudio Corian, Luigi Delle Rose, Elizabeth Gould, and Kostas Skenderis » Observational Tests of Holographic Cosmology» arxiv.org/pdf/1607.04878v2.pdf
[33] https://en.wikipedia.org/wiki/Small-angle_approximation
[34] QUANTUM -MECHANICAL PROBABILITIES AS SUMS OVER PATHS G. V. RIAZANOV
http://jetp.ac.ru/cgi-bin/dn/e_016_04_0909.pdf
[35] A. L. Dmitriev, V. S. Snegov The Weighing of a Mechanical Gyroscope with Horizontal and Vertical Orientation of the Spin Axis. Measurement Techniques, Vol. 44, No 8, pp 831 — 833 (2001)
[36] https://phys.org/…/2016-12-verlinde-theory-gravity.html…
[37] Resolving the Vacuum Catastrophe: A Generalized Holographic Approach*
Nassim Haramein, Amira Val Baker
Hawaii Institute for Unified Physics, Kailua Kona, HI, USA
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/
[38] «Gravity and Quantum Theory: Domains of Conflict and Contact»
T. Padmanabhan arxiv.org/pdf/1909.02015.pdf
[39] Probing cosmic isotropy with a new X-ray galaxy cluster sample through the LX–T scaling relation
