Текст презентации
Модульный генератор гравитационных сил (МГГС) — устройство преодоления гравитации. (Краткое описание).
Одним из главных моментов в описании проекта МГГС является то, что голографический принцип, предложенный в 1993 году нидерландским физиком-теоретиком Герардом ’т Хоофтом и дополненный американским физиком Леонардом Саскиндом, открывает естественный механизм искусственного генерирования гравитационных сил. Рассмотрим по пунктам такую возможность, опираясь на известную статью нидерландского физика Э. Верлинде: “О природе тяготения и законов Ньютона” [3].
«Мы утверждаем, что центральным понятием, необходимым для вывода гравитации, является информация. Более точно, речь идет о количестве информации, связанной с материей и ее распределением, независимо от вида конкретной микроскопической теории измеряемом в терминах энтропии. Изменения этой энтропии при перемещении материи приводит к появлению энтропийной силы, которая, как мы покажем, приобретает обличье гравитации» [3]. [Стр. 1. 12 строка].
- «В некотором смысле мир является двумерным, а не трехмерным, как предполагалось ранее»[2]. [Стр. 2. 9]. «В пределе очень большой области поверхности, ограничивающей пространство может быть принято, что вся эта поверхность плоская на бесконечности. В некотором роде, явления происходящие в трехмерном пространстве могут быть спроецированы на далекий «проекционный экран» без потери информации»[2]. [Стр. 3. 18 ].
Поскольку все явления могут быть спроецированы без потери информации, то голографический принцип может быть применён ко всей Вселенной [1], [2], и, значит, все явления, в том числе и силовые взаимодействия происходят на её голографической поверхности — экране.
2. «Но со времен Ньютона известно, что сила должна быть связана с ненулевым ускорением. С другой стороны, ускорение и температура тесно связаны. Наблюдатель в ускоренной системе отсчета обладает температурой Унру» [3]. [Стр. 4. 11 строка]. Распределение такой температуры на поверхности Вселенной крупномасштабно представлено известной анизотропией (диполь с температурой) [4] [Стр. 1309. 2-й столбец 9 строка снизу]. Другими словами, одна половина Вселенной отличается от другой — температурой».
3. «Итак, мы заключаем, что ускорение связано с градиентом энтропии. Это будет одним из наших главных принципов» [3]. [Стр. 6. 7 строка снизу].
Поскольку мы рассматриваем физику на поверхности с одной координатой времени, то нас будут интерисовать искусственно производимые ускорения ротора необычного гироскопа и проекции этих ускорений на голографический экран — космологический горизонт Вселенной.
4. Современная физика основана на так называемом принципе наименьшего действия. Он указывает на то, что существует некоторая величина, такая, что можно найти связанный с ней некикий минимум. Мы построим систему параметрических уравнений описывающих не координаты и траектории, а угловые трёхмерные перемещения каждой точки ротора независимые от радиуса. Поместим центр ротора в начало неподвижных декартовых осей (относительно ускоренного наблюдателя) и будем производить сферические вращения ротора минимальными угловыми перемещениями вокруг каждой из осей декартовых координат (триадами), за минимальные промежутки времени. Другими словами: рассмотрим замкнутую систему — модель силового астатического гироскопа, в котором сферический керамический ротор сферически движется вокруг одной неподвижной точки, в вакууме, внутри сферического статора, который, в свою очередь, связан с конструкцией находящейся, например, на поверхности земли.
5. Введём определение когерентного колебания, как основного элемента когерентной системы.
«Движение физического тела, при котором только одна его точка О остаётся всё время неподвижной, называется движением (вращением) твёрдого тела вокруг неподвижной точки О. В этом случае все точки физического тела движутся по поверхности концентрических сфер, центры которых находятся в точке О. Поэтому такое движение называют сферическим движением тела. Основываясь на определении сферического движения, получим параметрические уравнения когерентного колебания элементов массы из принципа наименьшего действия.
«Когерентные колебания элементов массы — это сферическое движение физического тела, полные колебания которого подчиняются гармоническим законам, последовательно сдвинутым на 90° и которые производятся вокруг неподвижных осей декартовых координат». Когерентные колебания элементов массы ротора гироскопа могут быть выполнены поочерёдно угловыми перемещениями θx, θy и θz его точек за минимальные и равные промежутки времени (микроциклы), соответственно, три микроцикла угловых поворотов образуют триаду (3t), серии которых, в свою очередь, образуют цикл,
Поскольку ротор гироскопа двигается сферически вокруг одной неподвижной точки, то его элементы массы двигаются по множественным концентрическим сферическим поверхностям.
Получим параметрические уравнения когерентного колебания из принципа наименьшего действия.

Параметры Θ = πt и -1 ≤ t ≤ 1; где Θ геометрический угол, отмеряемый по произвольному направлению часовой стрелки, начиная от соответствующей полуоси, а t задаёт необходимую точность угловых поворотов.
Согласно п. 3., пучности и узлы (градиенты) энтропии занимают постоянные позиции в пространстве и во времени цикла когерентных колебаний, что создаёт многослойную, интерференционную, информационную и когерентную систему.

Очень важно отметить, и как видно из графика когерентных колебаний ротора, поворотные ускорения его элементов массы связаны с осями неподвижных декартовых координат.
Поскольку ротор гироскопа когерентно колеблется (двигается сферически вокруг одной неподвижной точки), то каждый его элемент массы, в каждый момент времени, перемещается по своей замкнутой траектории лежащей на принадлежащей ему сферической поверхности, а вместе они двигаются по множественным сферическим концентрическим поверхностям, что можно расценивать как многочастичное квантовое явление. Как видно из графика цикла когерентных колебаний ротора ускорения Кориолиса или поворотные ускорения его элементов массы (αСi) связаны с осями неподвижных декартовых координат. Т. о., согласно п. 5., координаты значений ускорений элементов массы ротора в моменты времени когда (αСi) = 0 (их центры) связаны с осями неподвижных декартовых и занимают постоянные позиции в пространстве и во времени цикла и, значит, такая система обладает пространственной и временной когерентностью. Вся совокупность значений градиентов энтропии (ΔS), связанной с когерентным колебанием материи — элементов массы ротора, как уже отмечалось, при его локальной и постоянной температуре создаёт многослойную интерференционную и информационную систему.
Согласно пп. 1., 2., и 5 , утверждаем, что пучности и узлы (градиенты) энтропии (ΔS) на поверхности экрана занимают постоянные позиции, а их центры их (всего 6 шт.) связаны с осями неподвижных декартовых координат.
6. Управляя поворотами ротора, и производя смещения (αEi) элементов массы ротора вокруг двух из трёх осей неподвижных декартовых координат мы можем изменять положение центров градиентов энтропии (ΔS) на поверхности (Au). В этот момент смещения (заметания) градиентов энтропии по поверхности Au они распространяются без задержки во времени. «Это — естественный выбор, так как в этом случае весь экран использует ту же самую координату времени. Таким образом, обработка микроскопических данных по экрану может быть сделана, используя сигналы, распространяющиеся без временной задержки» [3] [Стр. 11. 1 строка снизу].
7. Т. о. рассматривая силы в выбранной нами замкнутой системе, описанной в п. 4., мы приходим к выводу о необходимости увеличить её до размера голографической поверхности Вселенной (Au) и такое право даёт нам голографический принцип, см. п. 1.

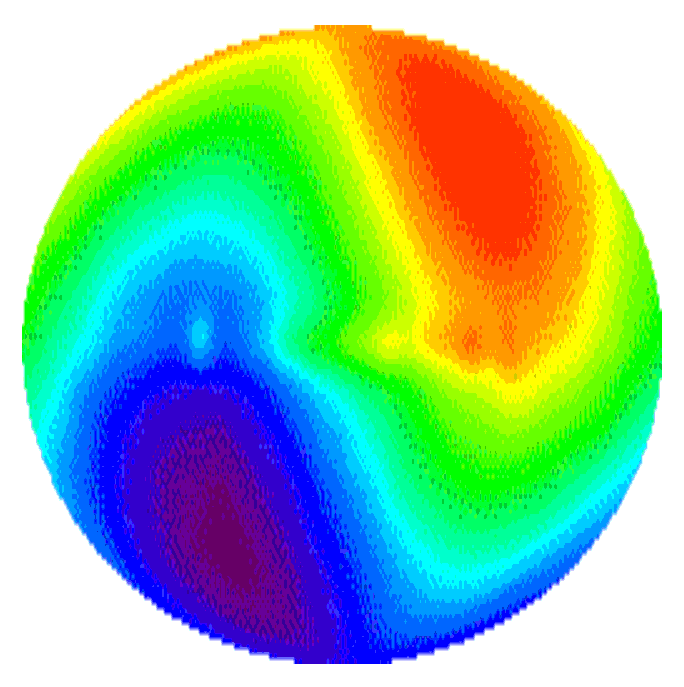
8. На рисунке, белыми кругами показаны центры интерференционной системы, представленной градиентами энтропии — шесть диаметрально расположенных на поверхности сферического ротора нулевых значений поворотных ускорений (αСi), которые связаны с неподвижными осями декартовых координат и проецируются на поверхность экрана. Дипольная анизотропия Вселенной крупномасштабно представлена градиентами её температуры (ΔTu) на голографической поверхности экрана и показана красным, зелёным и синим цветом.
9. Далее покажем, что гравитационная сила является энтропийной силой, обусловленной изменением количества информации, связанной с положением материальных тел (элементов массы ротора и внешнего окружения). Изменение положения центров пучностей и узлов (градиентов) энтропии (ΔS) на экране может быть выполнено за счет управляемого смещения (αEi) угловых перемещений элементов массы ротора, вокруг двух из трёх осей неподвижных декартовых координат, при постоянной локальной температуре ротора. В момент смещения (αEi) центры градиентов энтропии получают новое положение относительно внешнего окружения, возникает направленная энтропийная сила. Изменение положения на экране энтропии (ΔS) при перемещении элементов массы ротора приводит к появлению энтропийной силы, которая приобретает обличье гравитационной силы. см. [3]. «Мы должны заключить, что имеется только макроскопическое объяснение действия возникающей силы» [3] [Стр. 15. 18 строка]. Т. о. гравитационная сила может быть представлена как произведение глобального градиента температуры Унру (ΔT) на голографической поверхности, на градиент энтропии (ΔS), связанный с перемещением материи, за цикл когерентного колебания:
Fg = ΔTΔS.
Т. о., универсальный закон тяготения Ньютона — последствие статистически распределённых тепловых и энтропийных взаимодействий на уровне комптоновской длинны волны и непосредственно связанных с крупномасштабной анизотропией Вселенной.
10. В дополнении, можно предположить причину генерирования гравитационной силы за цикл когерентного колебания ротора. Диаметрально расположенные центры градиентов энтропии, в момент смещения, согласно п. 7, по-разному взаимодействуют с градиентами температуры (ΔT) на поверхности (Au), которая проявляется видимой анизотропией Вселенной [4]. Возникает направленная энтропийная сила, которая приложена к центру ускорения ротора и, которая, приводит к перемещению его центра масс и всей конструкции в выбранном направлении, связанного с неподвижными декартовыми координатами. Согласно п. 9, полученная энтропийная сила является направленной дальнодействующей гравитационной силой Fgrav, которая подчиняется второму закону Ньютона [3] [Стр. 13. 5 строка].
Для элементов массы когерентно колеблющихся ротора, направленная сила гравитации Fgrav применяется к центру ускорения.
Fgrav=ηmα²
где Fgrav — гравитационная сила
η — параметр порядка (1> η > 0) (обатная виличина термодинамического влияния среды(внешнего окружения)),
m — масса ротора,
α² = αCiαEi гравитационное ускорение (when αCi = αEi)
αCi — поворотное ускорение (ускорение, возникающее в результате когерентных колебаний).
αEi – ускорение смещения (ускорение возникающее в результате сдвигов элементов массы вокруг центра ускорений).
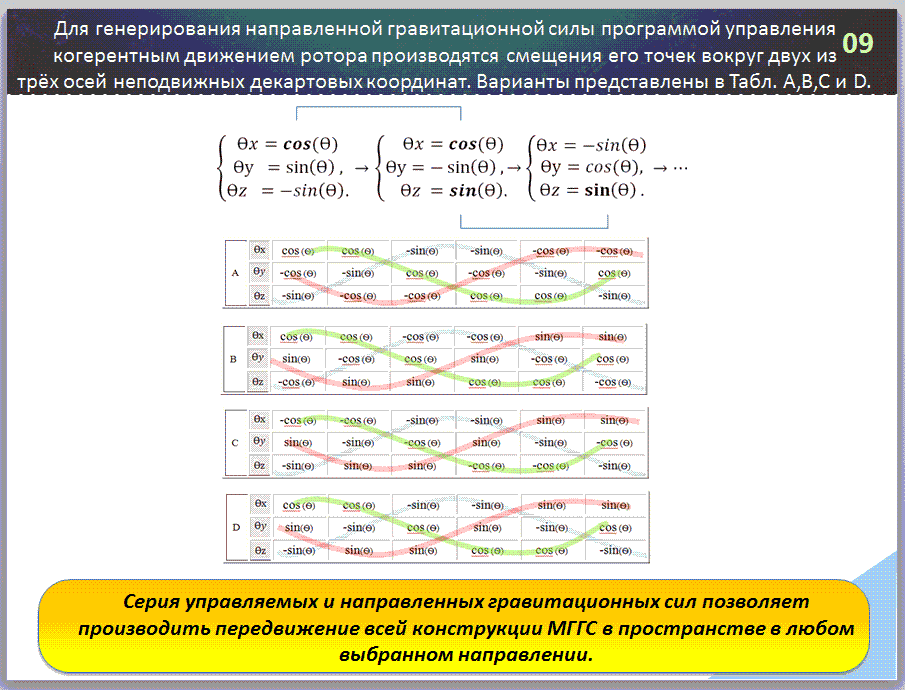
11. Примеры смещений угловых перемещений элементов массы ротора для генерирования направленных дальнодействующих гравитационных сил дано в таблицах A, B, C и D (в описании на сайте).
12. Серия управляемых и направленных дальнодействующих гравитационных сил позволяет производить передвижение всей конструкции в пространстве в любом выбранном направлении.
13. Согласно п. 7. Статор остаётся неподвижным по отношению к центру масс ротора и производит смещения элементов массы ротора, поскольку в состав замкнутой системы, ограниченной поверхностью (Au) входит всё внешнее окружение, в том числе и поверхность земли. Искусственно произведенные гравитационные силы являются дальнодействующими, противодействующими смещениям элементов массы ротора и приложены к его центру ускорений в полном соответствии с третьим законом Ньютона.
Выводы
Одним из главных моментов данной статьи является то, что голографическая гипотеза Г. ‘т Хофта — Л. Саскинда — Е. Верлинде подтверждается технически реализуемым прибором МГГС, созданным на основе первичных принципов: принципа найменьшего действия и принципа эквивалентности. Предполагается механизм, объясняющий статистическое возникновение гравитации, когда в естественных когерентных системах (при неизменной комптоновской длинны волны) на планковском уровне, распределение градиентов энтропии непосредственно связано с взаимодействием с крупномасштабной анизотропией Вселенной. Хотя этот вывод обладает кажущейся неочевидностью, тем не менее он подводит к предположению о том, что источником гравитации является пульсация проекций элементарных частиц атомного ядра при их взаимодействии с градиентами температуры дипольной анизотропии на поверхности Au. Т. о. гравитация – это внутреннее голографическое свойство вещества информационно представленного на анизотропной голографической поверхности Вселенной. Каждая «пульсация» проекций элементарных частиц информационно связана через взаимодействие с градиентами температуры дипольной анизотропии и с каждой частицей во Вселенной. Этим реализуется голографическое свойство: связь каждой частицы с каждой во Вселенной, через энтропийные силы на её поверхности и, т. о., связь макро и микромира через декогеренцию и обратно через рекогеренцию. Функциональная зависимость такой связи отражена во всез законах, втом числе и в законе Всемирного Тяготения.
Т. о., сила тяжести имеет термодинамический фон, и является энтропийный супер силой без соответствующего взаимодействия на микрофизическом уровне.
Проект MGGF содержит идеи с потенциально далеко идущими последствиями. Например, если сила тяжести является энтропийной силой на 2D поверхности, то, на самом деле, не было бы никакого смысла заниматься поиском микроскопической квантовой теории гравитации или искать объединения силы тяжести с другими микроскопическими силами в 3D пространстве за исключением энтропийных сил.
Литература
[1] G. ‘t Hooft, \Dimensional reduction in quantum gravity,» arXiv:gr-qc/9310026.
[2] L. Susskind, \The World As A Hologram,» J. Math. Phys. 36, 6377 (1995) [arXiv:hepth/
9409089].
[3] Verlinde, 2010] Erik Verlinde. On the Origin of Gravity and the Laws of Newton. arXiv:1001.0785v1 [hep-th] 6 Jan 2010. Русский перевод “О природе тяготения и законов Ньютона” перевод М.Х. Шульмана shulman@dol.ru http://timeorigin21.narod.ru/rus_translation/Gravity_and_entropy.pdf
[4] Дж. Ф. Смут III. «Анизотропия реликтового излучения: открытие и научное значение» Успехи физических наук. Декабрь 2007г Том 177 №12. (Нобелевские лекции по физике — 2006 г.)