Good afternoon friends! I an independent inventor from Ukraine — Alex Isakov. I ask you to forgive my English. Very short but strange problem. However, this study can lead to a fundamental breakthrough in science.
My invention is a fundamentally new type of gyroscope — an unusual gyroscope and his work is connected with the possibility of creating controlled directional forces to compensate and overcome gravity (anti-gravity). A difference between the operation of an unusual gyroscope as a device for overcoming gravity and similar devices is it’s not a contradiction with the fundamental laws of physics.
The reliability of information can be quite high if it comes from experimental data and at least three independent sources.
1. With reference to work an unusual gyro, from the position of classical mechanics:
The device is a sphere — rotor with magnets inside another sphere — a stator with inductors and a vacuum gap between them. The rotor rotates under the control of the computer (in the stator there are position sensors, drivers for providing pulses current big power ).
According to Euler’s rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible. However, for of full turnover of a physical body around three fixed Cartesian axes per cycle — possible.
If we load the equation of motion of the rotor into a computer simulator on the screen, we can see — rotation of the rotor per cycle occurs around three fixed Cartesian axes associated with the accelerated observer.
We can choose the average speed of rotation of the rotor The number of full revolutions per minute = 7000.
Proof of the unique properties of an unusual gyroscope, the rotor of which produces coherent oscillations in a vacuum we can demonstrate in the experimental data. We can see the non-electromagnetic, non-electrical and non-magnetic interaction of rotating non-magnetic disks in a vacuum. This can be called a thermodynamics force or new (yet unknown) force of interaction. Acceleration of the elements of mass in a vacuum causes significant entropic force. V. N. Samokhvalov “Non-electromagnetic Force Interaction in Presence of Rotating Mass in Vacuum.” The experimental data obtained in the vacuum apparatus demonstrate a significant 2.5N and action on the distance of entropic forces.
2. With reference to work an unusual gyro, from the position of Holographic Principle.
In the unusual gyroscope, the rotor mass elements acquire coherent oscillations that produce a fixed interference picture of the accelerations. Coherent oscillations and the interference pattern of the accelerated elements of the rotor mass of an unusual gyroscope can be related to a fundamental physical theory — the holographic principle. With such a formalism, the long-range action of entropic forces is not postulated but naturally arises from a holographic scenario.
3. With reference to work an unusual gyro, from the position of quantum mechanics.
If we load the equation all variants angular displacement of the rotor into a computer simulator on the screen, we can see dynamics and a lot of properties of every particle (60) of the Standard Model… .
All calculate means that an unusual gyroscope can be used in multiple applications (new types of instruments for research in quantum mechanics, cosmology, engines for controlling gravity …)
Please consider the variants of the possibility of prototyping an unusual gyroscope. Thank you, Alex Isakov
Thus, technically, we can reverse the arrow of time.
Let’s go back to the time machine. Moving in space, we do not move all the objects around us, we just move, which is extremely effective. The same with time. To move in time, it is enough to isolate a living object in the cabin from the external environment, and then exotic energy will not be required to move the entire Universe in time and known paradoxes will not arise. Such the time machine can be created on the basis of my invention — a local thermodynamic system — the third and last of the possible types of a power mechanical gyroscope with the maximum possible number of degrees of freedom in a mechanical holonomic system — Gyro_6DoF (previously unknown to science). More details about Gyro_6DoF design can be found on my page: https://www.facebook.com/groups/Unusualgyro
I am often asked the question: «what would such a time machine look like?»

Необычный гироскоп и симулятор для визуализации динамики проекций квантовых частиц
В науке существует однозначно мощное партнерство между теорией и инженерией. Это то, что дает нам атомную энергию, Большой Адронный Коллайдер и технологию космического полета и т. д. и т. п.. Теоретики говорят: «Теоретически это возможно». Инженеры затем выясняют, как заставить это работать. Они уверены, что математика является правильной, а теория работоспособной. Конечно, эти лагеря не являются взаимоисключающими. Теоретики пытаются понять инжиниринг, инженеры опираются на их глубокое понимание теории. Обычно это выглядит довольно гармонично, но иногда эти два мира сталкиваются. Теоретики утверждают, что практическое применение теории не представляется возможным, а инженеры утверждают: «Мы собираемся попробовать это в любом случае — этот «выстрел» стоит произвести».
Существует одна область науки, где как раз такой спор бушевал и продолжает бушевать уже в течение многих лет, пожалуй, самым спорным полем из всех областей науки/инженерии является контроль над гравитацией или управляемая гравитация. Огромная армия любителей и профессионалов непрерывно производят и загружают в интернет новые теории и описания экспериментальных моделей для решения фундаментальных проблем физики. В этом “угарном” процессе игнорируются базовые законы, легко постулируется возникновение дальнодействующей гравитационной силы из электрического, магнитного поля, некого эфира, СВЧ электромагнитных колебаний, или попросту, из ”несбалансированной” массы. Но законы физики неумолимы. С другой стороны, необходимо отметить, что без решения этих фундаментальных проблем физики в ближайшем будущем таких как создание технологий управления гравитацией, получение неисчерпаемой и экологически чистой энергии — энергии вакуума, преодоление скорости света в обмене информацией, цивилизация обречена на гибель. Например, сегодня нет технического решения для изменения траектории астероида или кометы, падающих на Землю. Всё, что предлагается для решения этой проблемы, приводит к непредсказуемым результатам, точнее, к большой вероятности гибели человечества, конечно, если ещё раньше, решая внутренние проблемы, оно само себя не вычеркнет из списка цивилизаций во Вселенной.
Физическая наука сегодня находится в довольно серьезном идеологическом кризисе. Кризис в физике продолжается уже несколько десятилетий, и его соответствующая глубина говорит нам о том, что мы находимся на пороге фундаментальных прорывов. Поэтому появление Голографического Принципа — новой нетривиальной идеи и использование ее для описания фундаментальных законов физики, выглядит естественным образом. Голографический Принцип изменит наши представления о самой природе пространства-времени, силе тяжести и откроет принципиально новый путь для управления гравитацией, получения неисчерпаемой энергии и обмена информацией без ограничения скоростью света. Сегодня Голографический Принцип — это сотни теоретических работ всемирно известных физиков: Г. т’Хофта, Л. Сасскинда, Д. Бекенштейна, Э. Верлинде, Х. Малдасена, Р. Буссо … . Уже имеются экспериментальные исследования, подтверждающие работу голографического принципа. С 1997 года было опубликовано более 10 000 работ, поддерживающих эту идею.
В отличие от любой другой теории, голографический принцип исходит из более фундаментального и первичного понятия — «информации на голографическом экране».
В 21-м веке информация лежит в основе всего. Информация — это количественная величина характеризующая систему. Интегральное представление информации (энергия) изначально несёт в себе потерю информации и не может претендовать на детальное описание окружающего мира. Информация сама по себе является объективной физической величиной в ряду других, таких как масса и энергия системы. Причём, речь идет о произвольных размерах физической системы, начиная с планковской площади с одним битом информации на ней и заканчивая голографическим экраном, с проекцией на нём космологического горизонта Вселенной. О космологическом горизонте нужно думать как о «раздувающейся сфере, не имеющей толщины», а «любое явление может быть спроецировано на её поверхность без потери информации» — Л. Сасскинд. Этот вывод очень важен для понимания сущности голографического принципа. Это означает, что любое искусственно созданное ускорение элементов массы без потерь проецируется на голографический экран Вселенной. Если голографический принцип работает, это означает, что вся информация о приемнике, передатчике, источнике энергии и всех наблюдателях, находится на одной голографической поверхности с единой коорднатой врмени и неважно где конкретно находится эта поверхность. Нам достаточно научиться искусственно проецировать и премещать информацию на этом голографическом экране — и мы решаем комплекс фундамнтальных проблем.
До появления голографического принципа не менее значимым было открытие анизотропии космического реликтового излучения (РИ), что произвело глобальный переворот в космологии и в физики в целом. Современные исследования РИ продолжают революцию в физике и космологии. Применение этого открытия для экспериментального доказательства голографического принципа в масштабах Вселенной сегодня выглядит закономерно в контексте соответствующей масштабности самого голографического принципа. Это первое, косвенное подтверждение голографического принципа, но возможна проверка голографической теории и в эксперименте.

Для достижения этой цели предлагается использовать необычный гироскоп МГГС (Модульный Генератор Гравитационных Сил). По сути это 3D компьютерный проектор ускорений (или проектор градиентов энтропии) на 2D голографический экран без потери информации. Его необычность оправдывается полными поворотами ротора за цикл вокруг трёх осей, а не вокруг одной оси, как у обычных гироскопов. В результате возникают когерентные колебания сферического ротора необычного гироскопа, которые производят неподвижную интерференционную картину из шести групп пучностей и узлов ускорений. Таким образом, согласованное поведение элементов массы ротора в вакууме организовано в кооперативное квантовое явление. Термодинамический механизм взаимодействия проекций ускорений когерентно колеблющихся элементов массы с глобальной температурной разницей на голографическом экране во время управляемого их перемещения объясняет возникновение энтропийной (гравитационной) силы, а серия управляемых гравитационных сил приводит нас к управляемой гравитации.Физика гравитации может получить новое развитие, подобное тому, которое оптика получила при переходе от тепла к источникам лазерного излучения.

У необычного гироскопа нет проблем с законами сохранения (с Третьим Законом Ньютона). Нет необходимости постулировать дальнодействие и возникновение самой гравитационной силы и подчинение её Второму Закону Ньютона (для случая искусственной генерации энтропийных сил). Гравитация естественным образом возникает в результате голографического сценария. Принцип причинности тоже не нарушается, т. к. размер замкнутой системы увеличивается до голографического экрана Вселенной с единой координатой времени. Более того, фундаментальные законы физики не постулируются, как делали их авторы, а математически выводятся из термодинамики на голографическом экране. Гравитация оказывается энтропийной силой, обусловленной изменением количества информации при перемещении проекций ускорений элементов массы по голографическому экрану с глобальным градиентом температуры на нём.
Серия управляемых и направленных гравитационных сил позволяет безреактивным способом производить перемещение всей конструкции МГГС в пространстве в любом из 60 –ти выбранных направлений за цикл когерентного колебания ротора.
Необычный гироскоп в качестве симулятора динамики проекций квантовых частиц на голографическом экране.
Сложность физических процессов на основе голографического принципа, например, исследования на уровне квантовых частиц атомного ядра и электронных оболочек требует создание эффективной пространственной модели компьютерного симулятора и экспериментальной установки для проверки современных физических теорий. Для визуализации квантовых процессов на базе необычного гироскопа был создан компьютерный симулятор динамики проекций квантовых частиц “IsAN”.
Современные исследователи рассматривают линию как одномерное пространство. Как только на линии ставится точка ноль, как начало координат, это означает на инженерном языке привязку этой линии к реальному пространству. Однако, в этом случае, назвать линию одномерным пространством означает нарушить закон сохранения информации голографического принципа, исключив точку 0 из множества. Развитие евклидовой геометрии показало, что основным ее элементом является не точка, а вектор, т. е. пара точек. Поэтому, если требуется рассмотреть переход по линии из -∞ через точку 0 к +∞, то необходимо обогнуть точку 0 по дуге ε и совершить оборот на угол Ѳ =±π.

Если игнорировать этот факт, называя линию одномерным пространством, то значит нарушить закон сохранения информации голографического принципа и, следовательно, заложить ошибку в основании физики. Если принять невозможность потерю информации как основу описания окружающего мира, то тогда необходимо принять тот факт, что линия терпит разрыв в точке начала координат, какой бы минимальный радиус дуги ε→0 не был, или в противном случае, это не может быть названо одномерным пространством.
Далее рассмотрим установившееся понятие двумерного (плоского) пространства. Если плоскость рисуется без начала координат, то это понятие не несет физического смысла. Если плоскость привязана к реальному пространству, то в ней фиксируется начало координат. В этом случае логика предыдущих рассуждений вступает в силу. Окрестность нуля не принадлежит этому двумерному миру. Окрестность нуля – выколотая точка на двумерном пространстве. Определение, ноль физически означает, что плоскость проколота лучом, исходящим из другого эмерджентного (возникающего) измерения. Последнее и утверждает, что плоскость несет в себе элемент эмерджентности пространства, это же утверждает и сам голографический принцип и это утверждение является его базовым содержанием. На этом процесс перехода в другие масштабные измерения заканчивается, поскольку согласно голографическому принципу, существует только одна поверхность с информацией – голографический экран вселенной. Таким образом, продолжая переход на плоскости из -∞ через точку 0 к +∞, мы должны снова огибать 0 по дуге ε для того, чтобы совершить оборот на угол Ѳ =±π. Аналогично, тому как мы огибали дугой точку 0 на линии, на плоскости мы можем дополнительно производить поворот координат вокруг точки 0, следовательно, каждая дуга ε будет описывать полусферу.

Если мы теперь устремим радиус дуги к нулю (ε→0), то физически, согласно термодинамике на сферическом голографическом экране, на квантовом уровне, решать по какой дуге производится поворот Ѳ =+π, или Ѳ =-π, на полюсе сферы будет последующее взаимодействие любой из двух проекций частицы с измерительным прибором (градиентом температуры), которое и фиксирует значение классических физических величин и распределение их вероятностей.
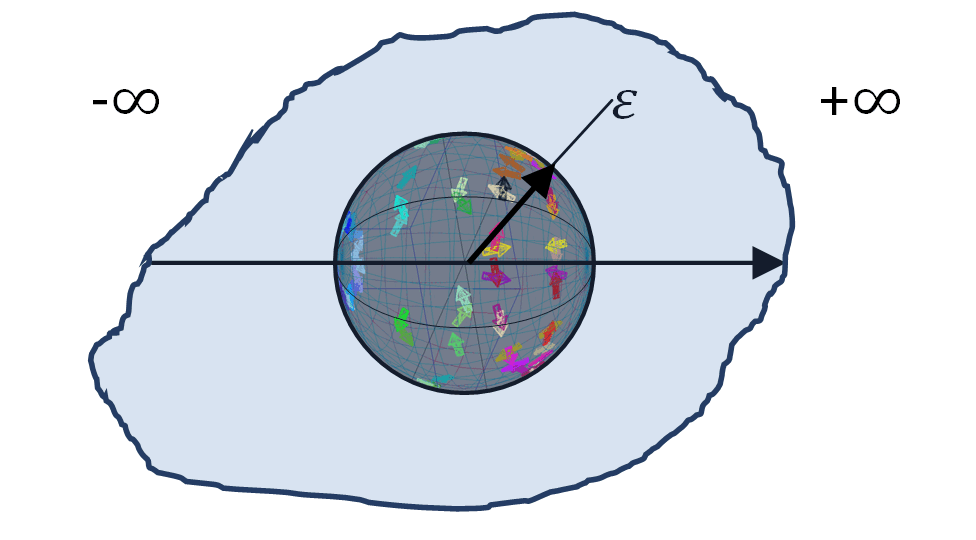
Голографический Принцип, на основе закона сохранения информации, позволяет производить проецирование любого явления на голографический экран Вселенной без потери информации. Поэтому, естественно, полученную нами сферу мы рассматриваем на голографическом экране Вселенной.
При такой геометрической и физической интерпретации абстрактное понятие точки, детализируются: каждая точка есть сфера. Таким образом, частица – точка, а статистические траектории пар проекций частицы — полюсов сферы естественным образом (из простой формулы когерентных колебаний) возникают на двух полусферах, принадлежащих одной сфере голографического экрана.
В квантовой механике частицы имеют внутренние степени свободы, которые в условиях изоляции термодинамической системы не связаны с движением частицы как целого. Динамика проекций частиц и взаимодействие между проекциями других частиц на голографическом экране и одновременное взаимодействие с глобальным градиентом температуры может визуализировать механизм приобретения свойств самих частиц, что и демонстрирует симулятор “IsAN”.
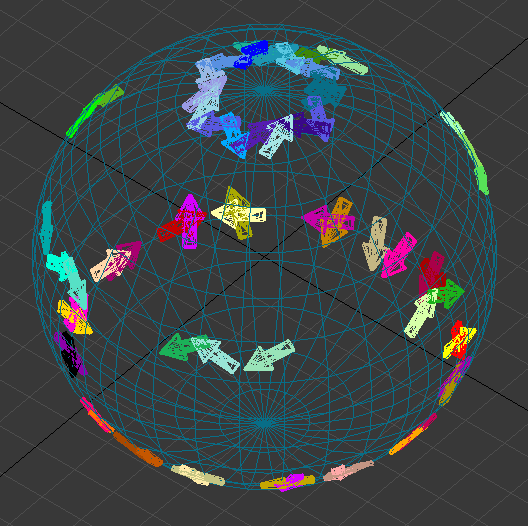
В симуляторе “IsAN” демонстрируются фрагменты компьютерных расчётов угловых перемещений — геометрического представления плотности вероятности некоторых проекций частиц построенных комбинациями когерентных колебаний из одной параметрической формулы.
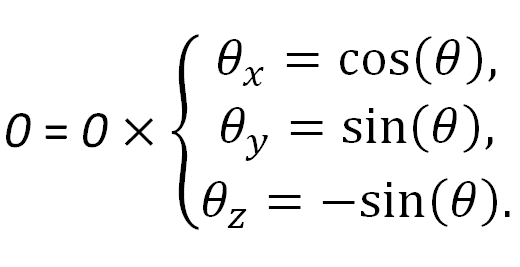
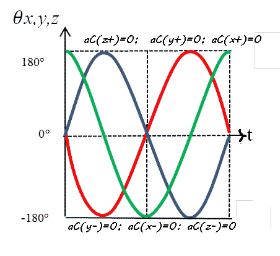
Где углы: θx — крен ; θy — тангаж ; θz- рысканье. Параметры θ= πt и -1 ≤ t ≤ 1; где θ — геометрический угол, отмеряемый, начиная с произвольного направления часовой стрелки, от соответствующей полуоси, а t задаёт необходимую точность угловых поворотов. Формула движения проекций частиц по голографическому экрану задана параметрически и применима для любого радиуса. В таблице представлены все 64 варианта комбинаций угловых перемещений минус 4 специфичких, где разность фаз равна нулю.

Мы отождествляем один бит информации с одной из фаз когерентных колебаний как фундаментальный бит естественного кодирования информации на одной площади планка сферического голографического экрана. Но уже две площади планка несут информацию из трёх бит, поскольку согласно термодинамике на голографическом экране, энтропия расширяющегося голографического экрана, естественным образом, измеряет и кодирует информацию, генерируя энтропийную силу. Информация представлена градиентами температуры, которые сохраняются и перемещаются по экрану и градиентами энтропии. Таким образом, всего шестнадцать байт информации кодируют все возможные траектории проекций элементарных частиц и античастиц.
В симуляторе стрелка обозначает проекцию частицы на голографический экран вселенной. В физическом смысле, стрелка на сферическом голографическом экране это направление локального градиента температуры вектор между двумя центрами любых двух, предварительно выбранных, соседних площадей планка. Пара диаметрально расположенных проекций на сферическом экране, в центре проекций, образуют возникающий объект — элементарную частицу.
На симуляторе “IsAN” можно наблюдать картину, в которой существуют пары диаметрально расположенных проекций частиц, которые сами по себе не имеют массы. Дадим этим проекциям частиц имена: «Is» и «AN». Будучи безмассовыми проекциями, они перемещаться по диаметрально противоположным участкам голографического экрана без ограничения скорости света, однако вместо этого на симуляторе можно наблюдать, что они «качаются» взад-вперед на нём, причем движение вперед частицы «Is» непрерывно превращается в движение назад частицы «AN», и наоборот. Фактически, это есть реализация на голографическом экране явления, называемого в квантовой физике как «zitterbewegung» («дрожание») и состоящего в том, что мгновенное движение, например, электрона из-за участия в таких колебаниях всегда происходит со скоростью света, хотя полное усредненное движение электрона характеризуется скоростью, меньшей скорости света. Каждый из указанных ингредиентов имеет спин величиной 1/2ℏ в направлении движения, соответствующий левому вращению в случае проекции частицы «Is» и правому для проекции частицы «AN». Реальное движение проекций электрона «Is» и «AN» слагается из большого числа таких отдельных процессов, так что наблюдаемое движение электрона можно рассматривать как результат некоторого их «усреднения» (хотя, строго говоря, здесь имеет место квантовая суперпозиция).






После запуска симулятора на сферическом экране видны особые точки — полюса сферы и точки скопления, расхождения проекций частиц. Их можно идентифицировать как особые точки взаимодействия частиц (электромагнитное, сильное и слабое) и как узлы образования сложных составных частиц. Для составных частиц, часть проекций состоит из более сложных наборов их траекторий. Более сложные составные частицы, выражаясь физическим языком, имеют большее количество «намоток» проекций на поверхности сферы голографического экрана.
Каждому фундаментальному фермиону соответствует античастица с такой же массой. Все заряды антифермиона противоположны. Проекции античастиц, перемещающихся «назад по времени» тоже важны для исследования, но они пока исключены из рассмотрения в симуляторе.
Одним из аргументов в пользу достоверности компьютерной симуляции динамики проекции частиц является её естественное возникновение из одной лаконичной параметрической формулы когерентных колебаний. Первое, что наблюдается на симуляторе “IsAN” после его запуска, это динамика проекций частиц трёх поколений на возникающем сферическом экране. Естественным образом возникает и общее число простых частиц в симуляторе, которое ровно 60+4 специфических. Стандартная Mодель элементарных частиц описывает 61 частицу (последним был обнаружен бозон Хиггса).
Этот вывод говорит нам только о том, что результаты наблюдения на компьютерном симуляторе за динамикой проекций частиц, требуют проверки на действующей модели необычного гироскопа.
Фундаментальные кирпичики, из которых строится материя, не ограничиваются электронами и двумя кварками. Помимо заряженного электрона надо добавить нейтрино — как копию электрона, только без заряда и почти без массы. «Почти» необходимо учитывать, поскольку глобальный градиент температуры имеет плоский рельеф на голографическом экране. Рельеф глобального градиента температуры по-разному взаимодействует с взаимодействующими между собой проекциями частиц на экране, что придаёт в центре проекций — частицам различную массу. Этот механизм и для множества различных частиц материи, согласно термодинамике на голографическом экране, отвечает за возникновение энтропийной силы, которая приобретает обличие всех известных фундаментальных сил и взаимодействий.
Из закона инерции следует свойство траекторий свободных тел — «прямизна», т. е. сохранение углов, а отсюда вытекает евклидовость геометрии пространства. Таким образом, мы видим, что не только в общей теории относительности, но и в классической механике геометрия навязывается динамикой — законом инерции, т. е. существованием массы. Становится понятным, как и почему возникают составные частицы (как число намоток траекторий пар проекций на сферу без толщины). Становится понятным, почему масса составных частиц может быть выражена через массу электрона. Все становиться на свои места, если мы в таком голографическом формализме позволим использовать принцип Маха или, другими словами, спроецируем на сферу, которую мы получили, температурный диполь анизотропии Вселенной. Голографический Принцип позволяет производить проекцию явлений в трёхмерном пространстве без потери информации на голографический экран Вселенной и неожиданно отражает надежды Эйнштейна. При создании Общей Теории Относительности Эйнштейн надеялся, что принцип Маха будет воплощаться в его теории, но этого не произошло. Существование инерциальных систем отсчета имеет сложный вопрос: в действительности ли, все объекты во Вселенной влияют на опыт, полученный в лаборатории на Земле? И далее: «… точка зрения, что имеет значение только ускорение по отношению к неподвижным звездам — это и называется принципом Маха. Теперь на этот вопрос есть ответ: каждая область оптической голограммы и голограммы Вселенной несет информацию обо всем объекте. В этом случае вся Вселенная — это объект, который взаимодействует с каждой своей точкой, а в каждой точке можно найти очертания Вселенной. Хорошо известный парадокс «тонкой настройки», который теперь раскрывается в этой глубокой глобальной отрицательной обратной связи, демонстрирует гораздо более высокую вероятность для возникновения и существования нашей Вселенной с её параметрами (которые мы наблюдаем). Теперь принцип Маха, как и Голографический Принцип, может быть экспериментально подтверждён в результатах исследований на симуляторе и эксперментально на практике — в необычном гироскопе.
На симуляторе мы можем наблюдать существование четырёх фундаментальных фермионов первого поколения. Однако помимо первого поколения есть ещё два. Как видно, проекции частиц второго и третьего поколений по всем свойствам аналогичны соответствующим частицам первого поколения, однако каждое следующее поколение тяжелее предыдущего. Динамика проекций частиц на сферическом экране даёт нам ключ к индитификации частиц в симуляторе, и позволяет детально рассмотреть свойства каждой частицы.
Для улучшения визуализации на симуляторе три поколения частиц выделены тремя спектрами: зелёным, синим и красным. В теории великого объединения частицы: кварки (u, d) и лептоны, группируются в три поколения: кварки (u, d) с электроном (e^-) и электронным нейтрино (ν_e) образуют первое поколение, кварки (c, s) с мюоном (μ^-) и мюонным нейтрино (ν_μ) образуют второе поколение, и кварки (t, b) вместе с тау-лептоном (τ^-) и тау–лептонным нейтрино (ν_τ)– третье поколение:
Массы кварков и лептонов растут с увеличением номера поколения. Заряженные лептоны — электрон (e^-), мюон (μ^-) и тау-лептон (τ^-) —можно считать тремя разновидностями электрона с различной массой(0,511, 105,658 и 1777 МэВ соответственно). Поскольку множество проекций частиц в симуляторе отличаются положением и числом намоток на сферический голографический экран относительно глобального градиента температуры, то это может объяснить тот факт, что масса некоторых частиц может быть приблизительно выражена через массу электрона. Мы приводим фрагмент из книги выдающегося физика современности Леонарда Сасскинда « Космический ландшафт»:
«Вот список масс элементарных частиц, входящих в Стандартную модель, выраженных в массах электрона. Все значения приблизительные.

Мы не видим никакой очевидной закономерности кроме той, что массы увеличиваются по мере того, как мы спускаемся вниз по списку.
Числа не выглядят связанными ни с какими математическими константами типа π или квадратного корня из двух. Единственная наблюдаемая закономерность возникает исключительно из-за того, что я намеренно отсортировал частицы в порядке возрастания масс».
Обратите внимание, что:
электрон, u-кварк и d-кварк — пропорциональная масса этих частиц говорит о том, что их проекции пересекаются по месту красного (температуры) на фотографии из космоса. Следует отметить, что это тип элементарных частиц — основная составляющая вещества. Поэтому их пропорциональные следы четко видны. Это подтверждение того, что наш подход имеет смысл. Любой пиксель голограммы коррелирует с информацией на всем экране. Это свойства голограммы.
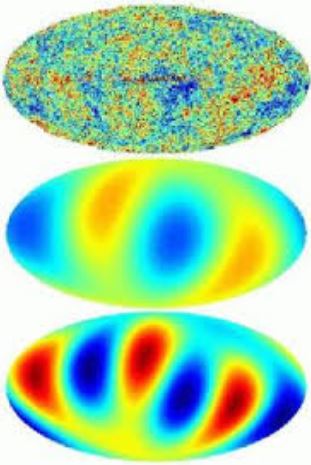
Решение этой задачи Леонарда Сасскинда может быть началом исследования фундаментальных квантовых процессов на компьютерном симуляторе «IsAN», так и в эксперименте, на основе действующей модели необычного гироскопа.
Вернёмся от компьютерного симулятора к рассмотрению работы электромехатронного устройства — необычного гироскопа.

Исскуственно получая гравитационную силу, мы имеем информацию о её направлении и величине непосредственно с голографической поверхности с единой координатой времени и, значит, без ограничения скоростью света. Таким образом, возможно создание на основе проекта МГГС голографически — гравитационных приемопередатчиков для возможности обмена информацией на любых расстояниях без задержки времени. Можно считать это лучшим перспективным направлением. Канал для такого обмена информацией — космологический горизонт Вселенной — ее голографический экран. Это означает, что существует возможность обмениваться информацией на расстоянии десятков миллиардов световых лет голографически — гравитационным способом без ограничений скоростью света и не нарушая законов физики. Если существуют развитые цивилизации, они будут использовать именно этот канал связи.
В принципе можно не вникать в суть сказанного, но любопытство должно победить только потому, что гироскопы очень интересные устройства, а МГГС — это принципиально новый тип силового гироскопа, с новыми неизученными свойствами. МГГС — это всего лишь небольшое эелектромехатронное устройство, которое может занимать десятую часть вашего письменного стола.
Тем не менее, эта технология может быть расширена до значимого масштаба, она может произвести революцию и в космической отрасли. Космический аппарат больше не нуждался бы в сотнях килограммах или даже в тоннах топлива, чтобы оставаться на орбите или исследовать глубокое космическое пространство. Например, Международная Космическая Станция ежегодно сжигает примерно 4 тонны ракетного топлива, и к ней регулярно необходимо его транспортировать. Примечание. Стоимость одного килограмма ракетного топлива — 20 000 долл. США
Стрела времени и механизм объединения фундаментальных взаимодействий.
Введение
Вопрос о теории всего (TOE) или теории объединения всех фундаментальных взаимодействий (электромагнитного, слабого, сильного и гравитационного) в единую теорию, наверное, является одним из основных вопросов физики. Очень близко к решению этой задачи приблизился голографический принцип.
Идея голографического принципа сводится к следующему: некоторая удаленная двумерная поверхность – космологический горизонт Вселенной или просто голографический экран, содержит всю информацию, необходимую для полного описания нашего мира.
«В пределе очень большой области поверхность ограничивающая пространство может представлена плоскостью на бесконечности. В некотором роде явления, имеющие место в трёх размерном пространстве, могут быть спроектированы на отдаленный ”проекционный экран” без потери информации» [1] [page. 3. 18]
Как и в оптической голограмме, данные, представленные энтропийной информацией на инфляционном голографическом экране в центре проекций, создают трёхмерные объекты.
Проекции явлений в трёхмерном пространстве можно проводить и обратно на голографический экран. Но, что очень важно, сам процесс проецирования происходит без потери информации и без ограничения расстоянием и временем. Таким образом, голографический экран — космологический горизонт Вселенной это поверхность единой, текущей координаты времени на которой находится вся информация об окружающем нас 3D мире. Подобно персонажам на телеэкране, мы живем на плоской поверхности раздувающейся сферы без толщины, которая только кажется нам глубокой. 3D эволюция привела нас к тому, что мы не можем представить 2D поверхность без 3D пространства и, в этом ключевую роль играют возникающие, в результате голографического сценария, вместе с пространством-временем фундаментальные законы физики. Поэтому, голографический принцип с реально существующей одной 2D поверхностью и одной возникающей (emerge) голографической координатой, воинственно воспринимается частью научного сообщества, хотя, в сущности, он не противоречит известной Стандартной модели физики. Более того, сами фундаментальные законы физики не постулируются и не подгоняются под эксперимент, как это делали их авторы, а математически выводятся из законов термодинамики на голографическом экране [2]. Эти свойства доказаны голографическим принципом и хорошо согласуются со свойствами оптической голограммы. Отсюда может быть задан вопрос: что реально в оптической голограмме — плёнка с информацией или трёхмерное изображение? Физика однозначно отвечает, что её законы имеют больше смысла, когда написаны в двух измерениях, а не в трех.
Термодинамика на голографическом экране (hs) с размерностью «2 + 1» (2D).
Связь между энтропией и информацией состоит в том, что изменение информации ∆I связано с отрицательным изменением энтропии ∆S.
ΔI = — ΔS ».
Кроме того, «мы заключаем, что ускорение связано с градиентом энтропии. Это будет одним из наших главных принципов:» [2] [page 11. 14]. «Таким образом, мы можем выразить изменение энтропии через ускорение. Это будет одним из наших основных принципов». [2] [page 11. 22].
ΔS ~α
Рассмотрим температуру на голографическом экране:
T→∆T∆x, (1)
где Ths — температура на голографическом экране, ∆T- положительная или отрицательная разница температур в двух точках на единицу расстояния между ними — (∆x) ⃗ , это векторная величина. Минимальный предел расстояния равен длине Планка. Максимальный предел — это расстояние между двумя центральными точками лепестков глобальной температуры дипольной анизотропии Вселенной [3], спроецированной на голографический экран.
«Учитывая, что энтропия системы зависит от расстояния (∆x) ⃗, энтропийная сила Fentr может возникнуть в результате термодинамической связи с расстоянием» [2] [page 7. (3.7)]
Fentr Δx = TΔS; (2)
Fentr – принципиально, фундаментальная энтропийная сила может рассматриваться как признак того, что она реализуется на голографическом экране в диапазоне (∆x) ⃗ . Произведём замену (1) в (2).
Fentr = ΔTΔS; (3)
где Fentr – энтропийная сила ∆T — градиент температуры на голографическом экране, ∆S — градиент энтропии, связанной с ускорением проекций явлений на голографическом экране. Под влиянием энтропийной силы, центр проекций и совпадающий с ним центр ускорений перемещается в трёхмерном пространстве. Это фундаментальная энтропийная сила (супер сила) на голографическом экране, которая в результате естественного кодирования информации в возникающих пространственных расслоениях (как следствие стрелы времени см. ниже) может быть представлена четырьмя известными силами.
Экспериментальные данные [3], о существовании крупномасштабной дипольной температурной анизотропии Вселенной, даёт основание предположить, что попарное «без временной задержки» перемещение проекций диаметрально противоположных центров градиентов (пучностей и узлов) ускорений на 2D голографическом экране с его температурным градиентом ΔT (Tu) порождает направленный импульс для каждой из проекций явлений.
Энтропийная сила приобретает обличье и гравитационной силы в возникающем пространстве-времени. Поскольку гравитационная сила Fg доминирует на больших расстояниях, но очень слаба на малых масштабах, то её величина больше зависит от взаимодействия градиентов энтропии, вызванных ускорениями материи с глобальным градиентом температуры голографического экрана (проекции дипольной температурной анизотропии Вселенной).
Fg = ΔTΔS. (4)
Тогда Fg — направленная гравитационная сила, ΔT— глобальный градиент температуры на космологическом горизонте Вселенной, ΔS — градиент энтропии, вызванный ускорением материи. Следовательно, перемещение проекций явлений, в результате поворотных ускорений на 2D голографическом экране приводит к возникновению противодействующей и дальнодействующей направленной гравитационной силе в 3D пространстве. Это означает, что энтропийная сила производит смещение координат центра ускорений материи (частиц при квантовых сдвигах) и приобретает вид всех известных сил и гравитационной силы, в частности.
Стрела времени
С экспериментальной, т. е. с относительной, точки зрения важна физическая непротиворечивость голографической теории, т. е. ее согласие с относительными измерениями в 3D. Именно эта относительность и позволяет проанализировать возникновение пространства, времени, всех известных частиц как способ кодирования информации на 2D голографическом экране. Для обычных физических тел и нас с вами – наблюдателей в нашем классическом мире вся проецируемая о нас информация, в результате декогеренции, размыта на голографическом экране. Это значит, что каждая точка во Вселенной связана с каждой точкой и одновременно с глобальным температурным градиентом, известным как анизотропия Вселенной. Энтропия в такой «раздувающейся» замкнутой системе растёт. Ростёт и объём информации, прямо связанный с энтропией во Вселенной, что субъекивно воспринимается нами как направление стрелы времени. Термодинамическая стрела (возрастание информации-энтропии) и психологическая стрела (повседневное восприятие времени) всегда указывают в одном направлении. Информация записывается и сохраняется на голографическом экране как градиенты температуры, и эту записанную информацию невозможно уничтожить, что субъектвно воспринимается нами как прошлое время.
Как же возникает стрела времени? Она возникает как следствие инфляции поверхности голографического экрана и естественного роста энтропии-информации на нём. Инфляция голографической поверхности приводит к возникновению голографического направления и сопровождается красными смещениями. Этот процесс связан с некоторой процедурой огрубления, или дискретизации (coarse graining procedure) информации на голографическом экране, таким образом, потерянная информация дополняется кодированием третьей возникающей (emerge) голографической координатой. Решающим является то обстоятельство, что только конечное число степеней свободы или пространственных расслоений ассоциировано с данным объемом пространства, поскольку само пространство ограниченно конечной поверхностью голографического экрана, как утверждает голографический принцип.
Исходя из этого, число степеней свободы, в результате инфляции голографического экрана обозначим параметром q — (emerge) координатой голографического экрана — перпендикулярной к его поверхности. Координата голографического экрана, по определению, включает в себя все элементы пространства расслоения «слои» (fiber bundles). Зависимость q от времени определяет «квантовую траекторию» голографического экрана. Траекторию q(t) мы будем рассматривать как дискретное элементарное случайное событие. Для анализа кодирования информации на голографическом экране мы будем учитывать траектории, на которых знак времени может изменяться произвольным образом. Многозначность траектории приводит к тому, что голографический экран одновременно, т. е. в любой заданный момент t, находится во всех своих состояниях q. Множество всех таких траекторий q(t) составляет общее пространство W дискретных элементарных событий — реализаций случайного процесса. Каждому подмножеству пространства W соответствует физическое событие или физическая величина.
Как же происходит переход к классическому состоянию квантовой системы Вселенной?
Все дело в том, что каждая траектория голографического экрана, побывала как в настоящем, так и в будущем, пройдя по всем возможным траекториям. Вклад от всех траекторий, кроме одной единственной, классической, сократился в результате взаимодействия с классическим прибором – глобальным градиентом температуры на голографическом экране. Этот тот же квантовый механизм взаимодействия частицы с измерительным прибором, который фиксирует значение классических физических величин и распределение их вероятностей. Следовательно, существование принципа Гамильтона (принципа наименьшего действия) в классической физике является следствием существования глобального градиента температуры на инфляционном голографическом экране Вселенной. см Рис.1

Рис.1 Ассиметрия температур
Необычный гироскоп MGGF
Опираясь на принцип наименьшего действия, рассмотрим классическую систему. В классическом пределе описывается свободное движение системы вдоль классической траектории — прямой линии, или свободное её вращение вокруг неподвижной оси, или вокруг одной точки, при трёхмерном колебании, в этом случае траектории создаются равными и полными угловыми перемещениями точек вокруг каждой из трёх осей за цикл. Ключевые свойства – прямая линия и равные углы. Таким образом, существование стрелы времени можно рассматривать как следствие существования классических траекторий свободных частиц в возникающем пространстве, или отсутствием бифуркаций этих траекторий. Такие функции можно изучать, используя пространственные расслоения и свойства фрактальных множеств. Это заключение даёт нам ключ к рассмотрению (во фрактале на уровне яблок) всех возможных траекторий (частиц) как траекторий полюсов на сфере которые возникают в результате её когерентных колебаний. Такой способ позволяет рассмотреть двоичный способ кодирования информации на голографическом экране на примере работы уникального гибрида классического и квантового прибора – гироскопа MGGF, см Рис.2.

Рис.2
Когерентные колебания
Начнём с определения когерентного колебания классического тела.
«Движение физического тела, при котором только одна его точка О остаётся всё время неподвижной, называется движением (вращением) твёрдого тела вокруг неподвижной точки О. В этом случае все точки физического тела движутся по поверхности концентрических сфер, центры которых находятся в точке О. Поэтому такое движение называют сферическим движением тела. Основываясь на определении сферического движения, получим параметрические уравнения когерентного колебания элементов массы физического тела. «Когерентные колебания элементов массы — создаются сферическим движением физического тела, вынужденные полные сферические гармонические колебания которого последовательно выполняются угловыми перемещениями его точек за равные и малые промежутки времени на пересечении осей неподвижных декартовых координат, с поверхностями концентрических сфер по законам синуса и/или косинуса».
 (5)
(5)
Где углы: θx — крен ; θy — тангаж ; θz- рысканье. Параметры θ= πt и -1 ≤ t ≤ 1; где θ — геометрический угол, отмеряемый, начиная с произвольного направления часовой стрелки, от соответствующей полуоси, а t задаёт необходимую точность угловых поворотов. Формула движения (5) задана параметрически и применима для любого радиуса ротора. Таким образом, можно определить максимально возможное число направлений когерентных колебаний оно равно 2^6 – 4 = 64. Согласно определению когерентного колебания, все элементы массы физического тела движутся по поверхности концентрических сфер, вокруг одной неподвижной точки. Если сопоставить все точки физического тела с элементами его массы, то можно заключить, что мы имеем дело с кооперативным квантовым явлением связанного с ускорениями. Число возможных траекторий полюсов связаны с числом поворотных ускорений элементов массы, которые в свою очередь связанны с неподвижными декартовыми координатами. Поворотные ускорения пучностями и узлами формируют неподвижную интерференционную картину.
Рис.3.
МГГС или Модульный Генератор Гравитационных Сил.
МГГС или Модульный Генератор Гравитационных Сил.
С позиции механики MGGF это необычный силовой гироскоп, который может поместиться на десятой части поверхности вашего стола. Он предназначен для экспериментальной проверки Голографического Принципа и принципа Маха, и мы рассмотрим, как он функционирует. Если Голографический Принцип работает, то в результате мы получаем направленную и действующую на расстоянии гравитационную силу, а серия управляемых гравитационных сил приводит нас к управляемой гравитации и множеству практических результатов. Концептуально всё выглядит достаточно просто.
Необычность гироскопа MGGF заключается в том, что его сферический ротор в вакууме за цикл делает полный оборот вокруг одной неподвижной точки трёх осей декартовых координат по законам синуса и\или косинуса, а не вокруг одной оси как в обычных силовых астатических гироскопах. Вначале наши усилия направлены на левитацию сферического и сбалансированного ротора (MGGF) внутри сферического статора связанного с конструкцией. Вакуум позволяет нам частично термодинамически изолировать сферический ротор от влияния внешней среды и значительно уменьшить трение. Одновременно с левитацией ротора требуется производить полные сферические гармонические колебания под управлением многоядерной компьютерной системы управления. В результате ротор будет когерентно осциллировать. Когерентные колебания элементов массы в вакууме приводят к поворотным ускорениям. Поворотные ускорения своими направлениями связаны с неподвижными декартовыми координатами и из пучностей и узлов формируют интерференционную картину. Эта интерференционная картина из ускорений неподвижна и созданна на шести идентичных и фиксированных в каждом цикле диаметрально противоположных участках, на огромном множестве концентрических поверхностях ротора, образованных траекториями его элементов массы. Таким образом, когерентные колебания элементов массы ротора в вакууме представляют собой кооперативное квантового явление. В соответствии с Голографическим Принципом, мы можем сделать «проекцию» шести диаметрально расположенных на поверхности ротора участков интерференционной картины на «удаленный» голографический экран без потери информации. Строго говоря, «проекция» и не требуется, если мы понимаем, что все явления и так «живут» на этой «удаленной» поверхности – голографическом горизонте Вселенной (в полном соответствии с Голографическим Принципом), так что я беру эти слова в кавычки. И так, мы добились того, что есть шесть фиксированных тождественных и диаметрально противоположных участков групп ускорений элементов массы как градиентов энтропии на «удаленной» поверхности (поскольку, согласно голографическому принципу, ускорения связаны с градиентом энтропии на голографическом экране), мы видим их, например, как шесть белых кругов диаметрально расположенных на сфере.

Таким образом, информация об ускорениях элементов массы ротора представлена на диаметральных участках голографического экрана. Л. Сасскинд по поводу этого мог бы сказать: «Парадокс информации, воспринимаемой одновременно в двух разных местах, бросается в глаза, но внимательный анализ покажет, что тут не возникает противоречия». Дальше все просто. Мы можем управлять движением четырёх из шести групп градиентов энтропии на голографическом экране с помощью системы управления ротором. Кроме того, нам известна крупномасштабная (глобальная) температурная анизотропия Вселенной — голографического экрана. Примерно половина плотности энтропии (градиентов температуры) на голографическом экране отличаются друг от друга, так что две из четырех групп градиентов энтропии связанных с перемещением элементов массы испытывают различное взаимодействие с этими областями. Масштабное нарушение симметрии на космологическом горизонте — голографическом экране и результат ускорения элементов массы во время рывка (первой производной от ускорения), приводят к направленной энтропийной силе, которая приложена к геометрическому центру (для сбалансированного сферического ротора – к его центру масс, совпадающего с его геометрическим центром). Подсчёт числа направлений когерентных колебаний приводит к возможности выбора любого из 64 направлений генерирования гравитационной силы за цикл. В соответствии с голографическим принципом, изменения положения на экране информации/энтропии вызванной ускорением материи приводит к появлению энтропийной силы, которая приобретает обличье гравитации. Fg=ΔTΔS,
Где Fg – гравитационная сила, ΔT- градиент температуры на космологическом горизонте, ΔS – градиент энтропии, вызванной ускорением материи. После преобразований мы приходим ко Второму Закону Ньютона, это означает, что управление гравитацией может производиться без экзотических масс и энергий.
Если Голографический Принцип работает, мы можем генерировать ряд направленных дальнодействующих сил, (несмотря на то, что голографический экран «далеко» от нас).
Третий Закон Ньютона не нарушается, так как размер замкнутой системы увеличивается до голографической поверхности Вселенной.
Физика гравитации может получить новое развитие, подобное тому, которое оптика получила при переходе от тепла к источникам лазерного излучения.
Если сила тяжести является энтропийной силой, то нет смысла искать гравитацию и постулировать её дальнодействие в микроскопической квантовой теории гравитации, или находиться в поисках объединения силы тяжести с другими микроскопическими силами, кроме энтропийных.
Серия управляемых и направленных гравитационных сил позволяет безреактивным способом производить перемещение всей конструкции необычного гироскопа в пространстве в любом выбранном направлении. Получая гравитационную силу мы получаем информацию о её направлении и величине непосредственно с голографической поверхности без ограничения скоростью света. Таким образом, возможно создание на основе проекта MGGF, голографически — гравитационных приемопередатчиков для возможности обмена информацией на любых расстояниях и без ограничения скоростью света.
Точное число направлений для возможности генерирования гравитационной силы, котрые получаются из формулы когерентных колебаний ротора необычного гироскопа и самоподобие информационных структур в голограммах, наводит на мысль о совпадении числа частиц в Стандартной Модели. И действительно, используя когерентный закон эволюции (как простую формулу когерентных колебаний, отражающую статистическое поведение изолированных от внешнего окружения частиц), загрузив её в сертифицированный симулятор мы видим, как возникают на сферическом экране в изометрии и ведут себя в динамике элементарные частицы, как они обмениваются энергией, импульсом и зарядами и как они связывают друг с другом, чтобы образовать более крупные структуры из трех поколений. Когерентный закон эволюции может объяснить основные особенности ядерной физики, астрофизики, космологии и материальных наук. Со статистическими методами он объясняет основу термодинамики и многое другое. Дальнейшие логические цепочки рассуждений связывают это знание с химией, с науками о жизни и так далее. В видеоизображении сертифицированного симулятора после загрузки параметрической формулы когерентного закона эволюции из экватора голографического экрана можно наблюдать один цикл статистической динамики проекций частиц Стандартной Модели. Можно четко видеть конкретные колебания проекции частиц (64 шт. Точнее 60 + 4 специфических, предположительно безмассовых частиц) трех поколений, «zitterbewegung» и другие свойства. Тандем из симулятора и необычного гироскопа уже сегодня может позволить измерять, исследовать и демонстрировать процессы на квантовом уровне не прибегая к дорогостоющему оборудованию принципиально новым способом в масштабе недоступном на современных ускорителях.
Совокупность информации в проекте МГГС и совпадение теоретических результатов с данными полученными на ускорителях, в эксперименте подтверждает теорию голографической Вселенной и принцип Маха.
Можно ли получать и передавать информацию быстрее, чем свет?
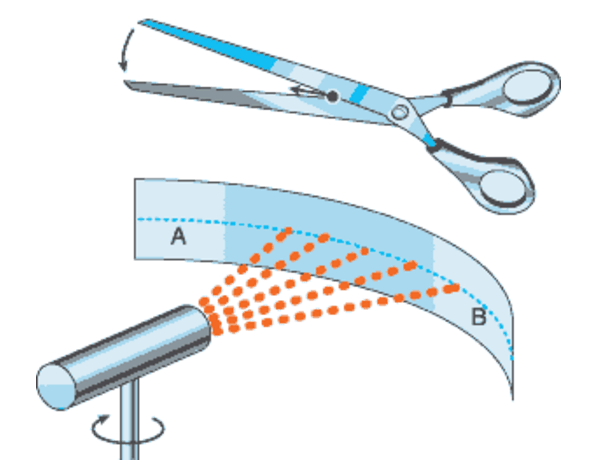
Даже людям, далеким от физики известно, что максимальная возможная скорость передачи данных любого сигнала равна скорости света в вакууме. Она обозначается буквой С и это почти 300 тысяч километров в секунду; точное значение C = 299,792,458 м / с. Скорость света в вакууме — одна из фундаментальных физических констант. Невозможность достижения скоростей, превышающих C — вывод из специальной теории относительности (СТО) Эйнштейна. Тем не менее, хорошо известная физическая теория — голографический принцип указывает на интересный феномен: информация-энтропия, вызванная ускорением материи, может быть спроецирована на космологический горизонт — голографический экран Вселенной без потери информации. Это означает, что в специально созданных условиях можно наблюдать сверхсветовую скорость передачи данных и принципы теории относительности не нарушается. Следует подчеркнуть, что «запрет» теории относительности применяется только к движению материальных тел и сигналов. Во многих других ситуациях, возможно движение на любой скорости, но это не движение материальных объектов и сигналов, а только их проекций. Если взять, к примеру, фонарик (или, скажем лазер, дающий узкий луч) и быстро описать в воздухе дугу, линейная скорость светового пятна «зайчика» на небе будет увеличиваться с расстоянием и на достаточно большом удалении превысит C. Световое пятно перемещается между точками A и B со сверхсветовой скоростью, но это не будет передачей сигнала от A к B, поскольку световое пятно не несет никакой информации о точке А. Однако, все меняется если работает голографический принцип. Представьте себе необычный гироскоп, в котором сферический ротор уравновешивается в вакууме, а его ротор можно вращать в любом направлении под управлением компьютера вокруг одной неподвижной точки — центра масс. Если в обычном гироскопе ротор за один цикл делает один оборот вокруг оси, то в необычном гироскопе MGGF, ротор может сделать полный оборот вокруг трех осей. Элементы массы ротора — производят когерентные колебания, а ускорения направлены вдоль фиксированных декартовых осей. Мы имеем вращательные ускорения, которые, согласно голографическому принципу, проецируется на противоположных сторонах космологического горизонта Вселенной без потери информации. Пучности и узлы образуют интерференционную картину из шести одинаковых секций. Они являются аналогами нашего светового пятна. Мы можем перемещать «зайчиков» в парах на экране, но теперь они представлены самой информацией, которая движется без ограничения скорости света. Таким образом, задача перемещения информации быстрее, чем скорость света может быть решена в необычном гироскопе MGGF. Для получения информации без ограничения скоростью света достаточно произвести измерение энтропийной силы, которая будет приложена к центру ротора. Эта некомпенсированная энтропийная сила, которая приложена к центру проекций и возникает в результате взаимодейчтвия градиентов энтропии, вызванной ускорением элементов массы ротора и градиентов температуры на голографическом экране.
Fentr = ΔTΔS;
где Fentr – энтропийная сила ∆T — градиент температуры, ∆S — градиент энтропии, связанной с ускорением проекций явлений на голографическом экране.
Если во Вселенной есть разумные цивилизации, они будут пользоваться именно этим каналом связи.

Голографический принцип, экспериментальная проверка на компьютерном симуляторе и необычном гироскопе
Физические теории созданы для описания реального мира, но без экспериментального подтверждения остаются только теориями. Например, Теория Относительности фактически стала инженерной наукой. Благодаря развитию технологии ускорителей стало возможным рассеивать очень легкие частицы, такие как электрон, протон, атомные ядра, и для этого мы используем ультрарелятивистские скорости. Эти эксперименты ежедневно проводятся на ускорителях во многих научных центрах, и не один из них не показал никаких отклонений от основных следствий теории. Тоже происходит и с фундаментальной теорией — Голографическим Принципом, который последовательно включает в себя Теорию Относительности и Квантовую механику и вскоре может стать не только инженерной наукой но и фундаментом Теории Всего на основе когерентного закона эволюции.
Сегодня Голографический Принцип — это сотни теоретических работ известных физиков мирового класса: Г. ‘т Хоофта, Л. Сасскинда, Я. Д. Бекенштейна, Э. Верлинде, Х.М. Малдасены, Р. Буссо … [1, 2, 3, 4, 5] . Уже есть экспериментальные исследования, подтверждающие работу Голографического Принципа [7,8] . С 1997 года опубликовано более 10 000 работ, поддерживающих эту идею.
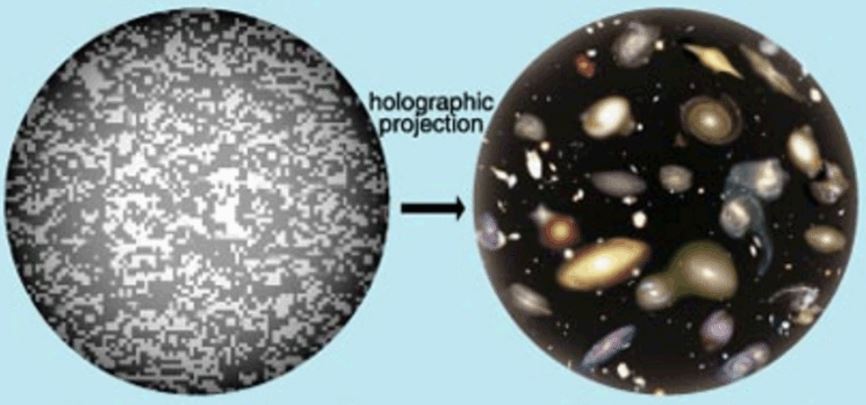
http://www.medbherenn.com/holographic-principle.html
Одним из сюрпризов современной физики было открытие того, что мир является своего рода голографическим. Но еще более удивительным было то, что количество пикселей (бит), которые содержит эта голограмма, пропорционально площади поверхности, окружающей описанную сцену, а не ее объёму. Другими словами: все, что есть, например, в вашей комнате это голографическое изображение, записанное на двумерной поверхности стен — экране. То есть, на самом деле, вы и вся остальная обстановка комнаты — все это масштабная квантовая сферическая голограмма, записанная на поверхности, ограничивающая не только объем вашей комнаты, но и вообще – всей вселенной. В масштабах вселенной это сферический и ускоренно инфляционная (раздувающаяся) поверхность или экран. Эта голограмма на сферическом экране представляет собой двумерный массив крошечных пикселей, каждый из которых имеет размер порядка длины Планка! Конечно, природа квантовой голограммы и метод кодирования двухмерных данных сильно отличаются от характера обычных оптических голограмм, но у них есть общие черты: изображение трехмерного мира полностью зашифровано на двумерной поверхности. Например, изображение на экране вашего компьютера представляет собой двумерную поверхность, заполненную светящимися пикселями. Каждый пиксель передает информацию об интенсивности и цвете 2D-изображения. Фактические данные, хранящиеся в памяти компьютера, содержат информацию о цвете и интенсивности отдельных пикселей. Как изображение на фотографии, экран компьютера представляет собой плоский вид реальной трехмерной сцены. Какой способ кодирования необходим, чтобы надежно отображать информацию о трехмерном объекте, включая также информацию о его внутреннем содержимом? Ответ очевиден: вместо набора пикселей, заполняющих плоскость, нам нужен набор пространственных элементов — вокселей, которые заполняют объем отображаемой сцены. Воксель представляет значение данных на регулярной сетке в трехмерном пространстве. Как и в пикселях в растровом изображении, сами вокселы обычно не имеют своей позиции (их координаты не связаны с координатами носителя), в явном виде они закодированы вместе со своими значениями. Положение вокселя выведено на основании его положения относительно других вокселей (то есть его положение в структуре данных, составляющее одно объемное изображение). Заполнение пространства вокселями является гораздо более сложной задачей, чем заполнение поверхности пикселями. Например, если плоский экран компьютера имеет разрешение одной тысячи на тысячу пикселей, то для его заполнения вам понадобится миллион пикселей. Но если мы хотим заполнить объём, с тем же разрешением, то нам нужно 1000x1000x1000 = 1,000,000,000 миллиардов вокселов.

Однако естественный голографический метод записи информации на голографичеком экране вселенной преподносит нам сюрприз. Голограмма вселенной представляет собой определённым образом составленные пикселы (биты информации на поверхности) которое позволяет однозначно восстановить полное трехмерное изображение и все силы и взаимодействия, используя только миллион пикселей, а не миллиард. Такая эффективность естественного кодирования информации на голографическом экране предположительно связана с тем, что по каждой половине голографического экрана (строго по своей траектории) перемещаются проекции частиц (пара проекций 0 или 1, в зависимости от квантового измерения, это частица) и каждая из двух проекций испытывает разные энтропийные силы, взаимодействуя только с глобальным градиентами температуры и, таким образом, центр проекций — частица приобретает массу — это и есть воксел на площади планка. Каждая из двух проекций воксела может меняться местами с соседними проекциями соседнего воксела, этод механизм отвечает за запутывание и, в результате, за возникновение (emerged) суперпозиции энтропийных сил на голографическом экране. Т. о. возникает третья пространственная координата и все три известные силы. Гравитация — особенная энтропийная сила (как кооперативное квантовое явление) — результат перемещений множества проекций градиентов энтропии (возникающих ускорений материи) и взаимодействия с глобальными и локальными градиентами температуры на экране. Это предположение может быть подтверждено научным методом визуализации данных на сертифицированном программном симуляторе и в исследованиях измерениями энтропийных сил на квантовомеханическом устройстве — необычном гироскопе.
Интересно рассмотреть аналогию между оптической и энтропийной голограммой. Оптическая голограмма является двумерным изображением и требует когерентных источников света (для однослойных поверхностей), но содержит полную информацию о трехмерной сцене. Однако, если вы просто посмотрите на фотопластинку с изображением оптической голограммы, вы не увидите ничего значимого: изображение реального мира на голографической пластине искусственным образом закодировано. Для записи требуются два источника когерентных колебаний, а для воспроизведения требуется третий когерентный источник, освещающий всю однослойную поверхность голограммы. Мы можем предположить, что аналогичным образом от двух источников когерентных колебаний — пары одномерных струн возникает сферическая поверхность, а её естественное когерентное колебание и ускоренная инфляция это то, что и является третим источником когерентных колебаний. Доказательство этого предположения может быть тоже продемонстрировано на сертифицированном компьютерном симуляторе. Предельно простая формула когерентных трёхмерных колебаний, загружается в симулятор и изначально не содержит в себе формулу сферической поверхности. Сфера естественным образом возникает (emerged) из когерентных колебаний ранее выбранной любой точки в трёхмерном пространстве. Кодирование с помощью когерентных колебаний является общим свойством для всех видов голограмм как для оптических, так и для энтропийных. Отсюда возникает когерентность квантовой механики, которая подтверждает голографическую природу Вселенной.

Переход от квантового мира к классическому сопровождается возникновением направленных энтропийных сил как компенсация потери информации в результате запутывания пар проекций или в классическом представлении — декогеренции квантовых процессов на голографической поверхности. Возникает (emerged) термодинамика на поверхности. Энтропийные силы приобретают вид всех известных четырёх сил, в том числе и гравитационных сил. В результате квантовых измерений возникает стрела времени, и всего этого достаточно для возникновения (emerged) крупномасштабного трёхмерного мира из раздувающейся сферической голографической поверхности с естественным образом закодированной информацией. Способы кодирования информации естественным образом эволюционируют. Всё перечисленное субъективно воспринимается нами как трёхмерное пространство, хотя все информационные процессы находятся на голографическом горизонте вселенной.
Сам голографический горизонт Вселенной мало изучен, но предполагается, что он расположен за пределами космологического горизонта возможно даже двух или множества космологических горизонтов, если речь идёт о мультивселенных. Тем не менее, для нас сейчас это не так важно, потому что согласно Голографическому Принципу все явления в нашей Вселенной могут проецироваться на его поверхность и обратно в центр проекции (во всех точках пространства) без потери информации, а этот аспект можно использовать в практических целях уже сегодня.
.
Что даёт нам такой формализм применённый к описанию вселенной?
Возникает возможность математически вывести фундаментальные законы физики, а не постулировать их после падения яблока, что уже продемонстрировано в работах Э Верлинде [6]. Полевая физика возникает (emerded) в результате голографического сценария и является его следствием. Поэтому эквивалентно, но совершенно по другому без постулирования полей и экзотических частиц раскрывается механизм возникновения (emerded) массы. Объясняются парадоксы квантовой механики и времени. С практической стороны мы получаем техническую возможность общаться с цивилизациями в нашей вселенной без ограничения расстоянием и скоростью света. Возникает возможность безреактивного перемещения в пространстве, искусственно управляя гравитацией без нарушения фундаментальных законов. Контролируемая гравитация позволит нам, в условиях приближённых к земным, испытывая постоянное искусственное ускорение 9,8G, путешествовать к планетам, к далёким звёздам и галактикам за разумное время. Известная ускоренная инфляция голографического экрана вселенной может быть использована для получения неисчерпаемой энергии и преобразование её в экологически чистую электрическую энергию. Но уже сегодня исследователям можно применить научный метод визуализации данных на компьютерном симуляторе, работая в области квантовой физики, космологии, а завтра производить измерения принципиально новым способом, не прибегая к дорогостоящим ускорителям. И это далеко не полный список фантастических, но вполне практически реализуемых возможностей.

Фотография из видеодемонстрации динамики проекций частиц Стандартной Модели выполненной на компьютерном симуляторе по предельно простой формуле когерентных колебаний.
Компьютерный симулятор как научный метод визуализации данных
Если мы загрузим уравнение движения точки в компьютерный симулятор (программу), мы увидим динамику этой точки. Для этого возьмем любую точку во Вселенной и произведем ее угловые перемещения вокруг одной оси Декартовых координат. После загрузки формулы на экране компьютера в изометрическом виде мы можем наблюдать обычный круговой поворот точки по кругу. Ничего примечательного. Но уже интересным способом происходит поворот выбранной нами точки вокруг двух осей. Симулятор демонстрирует характерную динамику точки на возникающей (emerged) сфере и поворотные ускорения, которые направлениями связанны с неподвижными осями Декартовых координат. Но еще более удивительным является все возможные варианты угловых перемещений этой точки вокруг трех осей. Здесь подавляющее большинство экспертов будут выступать против такого заявления. Согласно теореме вращения Эйлера одновременное вращение вдоль ряда неподвижных осей в одно и то же время невозможно. Тем не менее, я обращаю ваше внимание, что для полного оборота точки или физического тела (ротора) вокруг трех фиксированных декартовых осей за цикл (цикл — это ключевое слово) вполне возможно. Раньше казалось это невозможным, и теоретическая физика упустила описание такого движения физического тела или точки. Симулятор демонстрирует это принципиально новое колебание точки и/или физического тела. В научной литературе описание таких колебаний отсутствует.
В это трудно поверить, но как только мы загружаем формулу угловых перемещений точки вокруг трех неподвижных осей, в соответствии с гармоническими законами, мы можем видеть возникновение (emerged) сферического экрана и проекций всех элементарных частиц Стандартной Модели на нём!
На экране компьютера можно видеть 60 пар проекций частиц, динамику их трёх поколений, их спины и феномен «zitterbewegung» … . Это эквивалентно тому, что вы подключили к телевизору генератор случайных чисел, занесли в него начальную комбинацию двоичного кода, и в результате, на экране вы вдруг увидели, например, свой любимый фильм.
После запуска симулятора на сферическом экране, в изометрии, видны особые точки — полюса сферы и точки скопления, расхождения проекций частиц. Их можно идентифицировать как особые точки взаимодействия частиц и как узлы образования сложных составных частиц. Для составных частиц, часть проекций состоит из более сложных наборов их траекторий. Более сложные составные частицы, выражаясь физическим языком, имеют большее количество «намоток» проекций на поверхности сферы голографического экрана.
Каждому фундаментальному фермиону соответствует античастица с такой же массой. Все заряды антифермиона противоположны. Проекции античастиц, перемещающихся «назад по времени» тоже важны для исследования, но они пока исключены из рассмотрения в симуляторе.
Поскольку множество проекций частиц в симуляторе отличаются положением и числом намоток на сферический голографический экран относительно глобального градиента температуры, то это может объяснить тот факт, что масса некоторых частиц может быть приблизительно выражена через массу электрона.

Если исследуемая нами точка принадлежит сферическому ротору гироскопа, то мы получаем необычный гироскоп. Вращение сферического ротора в вакууме вокруг трех декартовых осей за цикл имеет новые неизвестные свойства. Например, трёхмерные колебания ротора — когерентны и мы имеем неподвижную интерференционную картину из ускорений элементов массы ротора. Когерентность и интерференционный паттерн приводит нас голографии.
Если Голографический Принцип работает, то можно искусственно создать гравитационные силы дальнего действия, используя голографические свойства, например, кооперативные ускорения элементов массы ротора необычного гироскопа. Это устройство позволит нам контролировать гравитацию и иметь множество интересных приложений, причём, не нарушая фундаментальных законов физики.
Необычный гироскоп

Необычный гироскоп — небольшое квантовомеханическое и электромехатронное устройство, работа которого описывается в области между классической и квантовой физикой. Эта область раньше считалась пустой. Однако, устройство может занимать десятую часть вашего стола. Сферический ротор необычного гироскопа имеет магниты и вращается в вакууме внутри сферического статора с индукторами под управлением компьютера (имеются датчики и драйверы для создания вынужденных колебаний ротора). Название необычный гироскоп оправдано тем фактом, что его ротор производит полные вынужденные колебания одновременно вокруг неподвижной точки – центра масс и трех фиксированных осей за цикл. Это предельно простое параметрическое уравнение угловых перемещений для точек ротора необычного гироскопа:

Где θx, θy, θz последовательное угловое смещение любой предварительно выбранной точки на поверхности ротора вокруг соответствующих осей неподвижных Декартовых координат, связанных с ускоренным наьлюдателем. Параметры: θ = πt и -1 ≤ t ≤ 1; θ — геометрический угол, определяемый произвольным и предварительно выбранным направлением угловых вращений. Уравнение задается параметрически, и оно применимо для любого радиуса ротора. Мы можем задать максимальную точность угловых перемещений любой точки ротора, если Δt → 0.
Как только новый тип гироскопа был изобретен и тестировался на симуляторе, возник вопрос: какие новые свойства он может иметь?
Первое, что бросается в глаза, глядя на очень простое уравнение движения ротора, это то, что колебания ротора когерентны (обладают пространственной и временной когерентностью). Разность фаз таких колебаний является постоянной. Кроме того, используя симулятор, мы можем наблюдать фиксированную интерференционную картину из ускорений (α), связанных с фиксированными Декартовыми координатами. Мы видим шесть групп ускорений, которые диаметрально расположены и связанны направлениями с шестью полуосями Декартовых координат. Если вычислить все возможные комбинаций направлений угловых перемещений по гармоническим законам, то их число будет ровно 60.

Эскиз конструкции:
- Основание.
- Оболочка.
- Статор (фронтальный разрез по диаметру).
- Стойка.
- Ротор.
- Магниты (66 шт.).
- Магнитная точка.
- Оптическая точка
- Катушки индуктивности (66 шт.).
- Датчики (магнитные и оптические).
- Ведомые микроконтроллеры и драйверы катушек индуктивности (микромодуль).
- Компьютер.
- Аккумуляторы.
- Солнечные батареи.
- Внешние крепёжные болты (4 шт.).
- Кабель.
- Вакуумный микронасос (4 шт.).
- Цифровой вакууметр и электромагнитный клапан (4 шт.).
- Цифровой инфракрасный датчик температуры и предохранительный термоклапан (4 шт.).
- Крепёжные болты для полусфер статора (16 шт.)
Необычный гироскоп это принципиально новый тип гироскопа, который отличается от любых силовых гироскопов не только отсутствием механических осей и отсутствием газовой подушки, но и когерентными колебаниями сферического ротора в вакуумной полости статора. В то время как ротор традиционно приводимого в действие силового гироскопа совершает полное вращение вокруг одной и той же оси за один цикл, ротор необычного гироскопа вынужден быстро вращаться вокруг трех осей (Ox, Oy, Oz). Это его концептуальное отличие от любого гироскопа, и эта особенность отражена автором этого текста в формуле патентной заявки. Левитация ротора внутри статора достигается путем его активной электромагнитной подвеске под управлением компьютерной системы. Как правило, в трехосных гироскопах используется карданный подвес, который позволяет свободно вращать ротор относительно трех осей, и именно это делает их несколько похожими на необычный гироскоп. Но только похожими. Вынужденные и полные колебания ротора необычного гироскопа вокруг трех осей за цикл — это его принципиальное отличие от любого силового гироскопа.
Таким образом, за цикл когерентных колебаний ротор необычного гироскопа совершает один полный оборот вокруг одной неподвижной точки — это геометрический центр, центр масс и центр ускорений ротора и одновременно вокруг трех осей декартовых координат.

Триада
Например:
Нам дана точность угловых перемещений ранее выбранной нами точки на роторе: Δt = 1/360. Это означает, что мы начали делать угловые перемещения этой точки, в постоянном и минимальном временном интервале, на поверхности ротора примерно на один градус, например, согласно закону (Cosθ) и вокруг фиксированной оси x. В следующем равном и минимальном временном интервале мы можем производить угловые перемещения этой точки вокруг оси y, но уже по закону (Sinθ) и соответственно для z (- Sinθ). Но поскольку для каждой оси до конца цикла осталось около 359 градусов, то мы продолжим такими триадами последовательно производить угловые перемещения точки, которые в конечном итоге будут заканчиваться одновременно для всех функций, так как разность их фаз постоянна. Мы получили цикл когерентных колебаний. Нам пока еще не нужно знать, как ведут себя точки ротора, каковы их траектории. Функции чередуются и есть шесть групп направленных (мгновенных) вращательных ускорений, связанных с фиксированными декартовыми координатами. В пространстве и во времени цикла они занимают постоянные позиции. Таким образом, нами получены когерентные колебания всех точек ротора необычного гироскопа в вакууме и силы Кориолиса, действующих на каждый его элемент массы.
Принцип эквивалентности
Принцип эквивалентности говорит нам о том, что мы не можем отличить инерционную и гравитационную массу от эксперимента. Эйнштейн изобрел эксперимент с лифтом. Лифт бесконечно удален от гравитирующих тел в пространстве и движется с ускорением. Тогда все тела в лифте будут находиться под действием инерции и окажут давление на пол лифта. То есть тела будут иметь вес. Если лифт не движется, а висит над гравитирующей массой в однородном поле, все тела также окажут давление на пол в лифте. Таким образом, невозможно различать эти две силы. Поэтому все механические явления будут происходить одинаково в обоих лифтах. Эйнштейн распространил это утверждение на все массы физических тел во Вселенной. Если мы ищем способ контролировать гравитацию, и аксиома Эйнштейна позволяет нам не различать силы инерции и силы тяжести, мы должны воспользоваться этой возможностью и на практике использовать силы инерции, которые зависят от скорости. Например, это сила Кориолиса, которая отклоняет тело от прямолинейного движения, если эти тела находятся во вращающейся неинерциальной системе отсчета.
Сила Кориолиса
Величина сил Кориолиса зависит от угловой скорости ротора. Можно предположить, что суперпозиция сил Кориолиса, полученная таким образом, эквивалентна фиктивному «гравитационному» полю, действующему на каждый элемент массы ротора. Поскольку все силы Кориолиса равны друг другу и ортогональны, их сумма будет равна нулю и, значит, центр масс ротора останется неподвижным. Но мы можем увеличить эти силы Кориолиса за счет увеличения скорости когерентных колебаний ротора.
Кроме того, у нас есть возможность одновременно смещать все точки (все элементы массы), например, вокруг любых двух из трех фиксированных осей Декартовых координат, искусственно, и за короткое время, разрушая когерентные колебания при этом создавая кратковременную декогеренцию. И да, мы можем технически сделать это в конце каждого цикла, используя компьютерную систему управления движением ротора. В то же время мы не нарушаем Третий Закон Ньютона, пока мы не утверждаем, что центр массы ротора должен изменить свое положение в пространстве в такой замкнутой системе. Центр масс ротора должен остаться в полном покое при полном равенстве сил Кориолиса действующих на него, как при когерентных колебаниях ротора, так и в момент искусственно производимой декогеренции. Направленная гравитационная сила, согласно Закону Сохранения Импульса, не должна возникать.
Но совсем другое дело, если работает Голографический Принцип и его Закон Сохранения Информации, что косвенно подтверждается в экспериментах. Голографический Принцип это единственная фундаментальная теория, которая позволяет нам расширить размер закрытой системы до ее максимального размера — голографического экрана вселенной.
Закон Сохранения Информации и глобальная температурная анизотропия вселенной.

Для получения направленной гравитационной силы в необычном гироскопе нам необходимо найти анизотропию голографической поверхности и использовать законы термодинамики на голографической поверхности.
До возникновения Голографического Принципа соизмеримое с ним по масштабности, было обнаружение анизотропии Вселенной, известной как анизотропия космического микроволнового фона реликтового излучения РИ. По сути это крупномасштабная разница температуры в разных направлениях на небе [9]. Экспериментально подтверждённая дипольная анизотропия вселенной и открытие когерентных акустических волн, имеет большое значение не только для космологии, но и для всего естествознания в целом. Когерентность колебаний в ранней вселенной так же подтверждает голографическую природу вселенной. Можно сказать, что крупномасштабные трехмерные звуковые когерентные колебания в ранней вселенной действовали до периода рекомбинации и закончились через 379 000 лет после Большого Взрыва. Однако звуковые когерентные колебания не исчезли, а зафиксировали большой масштаб глобального градиента температуры на голографическом экране. Поэтому сегодня мы можем наблюдать глобальный градиент температуры вселенной фотографируя её со спутников в космосе.
Согласно Голографическому Принципу, мы можем производить проекцию РИ и проекцию градиентов энтропии, отражающей перемещение материи на голографический экран, без потери информации. Зафиксированный спутниками масштабный глобальный градиент температуры на голографическом экране – фундаментальный элемент, который взаимодействует с перемещающимися проекциями. Например, исследуя динамику проекций квантовых частиц на симуляторе, этот механизм взаимодействия глобального градиента температуры демонстрирует возникновение (emerged) массы у частиц, указывает на точное число элементарных частиц и число частиц, не обладающих массой (60 и 4, соответственно).
Для того, чтобы исследовать термодинамику на голографическом экране, мы должны учитывать влияние проекций РИ на динамику проекций ускорений элементов массы, перемещающихся по экрану. Рассматривая результаты работы симулятора, динамику проекций частиц мы учитываем эту разницу в температуре сферического экрана. Отсюда можно предположить, что Голографический Принцип может выявить новый голографический механизм генерации масс частиц и всех известных сил и взаимодействий. В качестве единой силы может выступить энтропийная сила, действующая на голографическом экране.
Контроль гравитации на основе необычного гироскопа.
Итак, примерно половина глобальных градиентов температуры на голографическом экране Вселенной отличается друг от друга, поэтому две из четырех групп градиентов энтропии (белые круги на фотографии) из-за движения элементов массы ротора при смещении, в момент искусственно произведенной декогеренции, испытывают разное по величине взаимодействие с этими областями. Крупномасштабное нарушение симметрии на голографическом экране и результат декогернции колебаний элементов массы ротора приводят к направленной энтропийной силе, приложенной к центру масс ротора необычного гироскопа.

Согласно голографическому принципу изменение этой энтропии при перемещении вещества приводит к энтропийной силе, которая принимает вид гравитационной силы.
Fg = ΔTΔS,
где Fg гравитационная сила,
ΔT – глобальный градиент температуры на космологическом горизонте,
ΔS — энтропийный градиент, возникающий в результате перемещения вещества
(смещений на голографическом экране проекций ускорений элементов массы ротора), ΔS ~ α.
После преобразований мы приходим ко второму закону Ньютона [6], а это означает, что гравитационную силу можно искусственно получать без экзотических масс и энергий, что приводит нас к контролю над гравитацией.
Таким образом, интегральный гравитационный эффект определяется множеством энтропийных сил, взаимодействующих с крупномасштабной (глобальной) дипольной анизотропией, представленной температурой на голографическом экране Вселенной. Гравитация — это термодинамическое явление. Ряд сгенерированных управляемых и направленных сил гравитации позволяет нам осуществлять смещение всей конструкции необычного гироскопа в пространстве в любом выбранном направлении нереактивным способом. Это означает, что для одной точки — центра и для всех точек, т. Е. Центра масс ротора необычного гироскопа, гравитация, например, гравитация Земли, может быть полностью компенсирована и / или преодолена. Сегодня многочисленные эксперименты с быстрым вращением массы в вакууме (7000 об/мин) демонстрируют дальние силы в 2,5 Н. Идея о том, что гравитационная сила может рассматриваться как действующая на расстоянии энтропийная сила, подтверждается в независимом эксперименте [10].
Выводы.
Если мы рассмотрим все возможных направления когерентных колебаний ротора необычного гироскопа, то их число будет ровно 60. Это число соответствует числу элементарных частиц Стандартной Модели. И действительно, после загрузки в сертифицированный симулятор чрезвычайно простой формулы, описывающей динамику ротора необычного гироскопа, на экране компьютера в изометрии можно наблюдать появление сферического экрана, а также динамику и свойства элементарных частиц. Принцип голографии заключает, что: гравитация объясняется как энтропийная сила. Принцип эквивалентности приводит нас к выводу, что на самом деле это закон инерции, происхождение которого энтропическое. Эта термодинамика на экране, возникающая из-за статистического поведения микроскопических степеней свободы локализованных на голографическом экране Вселенной. Таким образом, сила тяжести и его дальность не постулируются, а производятся из голографического сценария, и представляет собой результат естественной или искусственной декогеренции квантовых процессов. Этот же механизм, но без декогеренции ответственен за появление массы у частиц. Результатом кодирования информации на голографическом экране становится масса / энергия, гравитация и пространство-время. Необычный гироскоп можно использовать для детального изучения этого предположения. Ряд, созданных и направленных дальнодействующих гравитационных сил, позволяет нам контролировать гравитацию. Устройство, также, может ответить на вопрос: действителен ли Голографический Принцип, согласно которому физика нашего трехмерного пространства-времени эквивалентна физике термодинамике на двумерной поверхности. У нас есть простое уравнение движения для любой произвольно взятой точки во Вселенной. Уравнение, которое на сертифицированном симуляторе демонстрирует многие свойства частиц Стандартной Модели и само место, где действительно существует наш трехмерный мир — двумерный сферический голографический экран вселенной. Мы сталкиваемся с эквивалентностью свойства оптической голограммы, когда каждый пиксель голограммы несет информацию обо всём изображении или всех объектах вселенной. Работа необычного гироскопа описывается тем же уравнением. Это означает, что мы на правильном пути, экспериментальные данные подтверждают это. Научная визуализация данных подтверждает и необходимость срочного прототипирования модели необычного гироскопа.
Один из вариантов видео, полученное на компьютерном симуляторе из одного простого уравнения угловых перемещений любой точки во вселенной, вокруг неподвижных Декартовых осей координат.
Литература
[1] J. M. Bardeen, B. Carter, and S. Hawking, “The four laws of black hole mechanics,” Commun.Math.Phys. 31 (1973) 161–170.
[2] J. D. Bekenstein, “Black holes and entropy,” Phys.Rev. D7 (1973) 2333–2346.
[3] S. Hawking, “Black Holes and Thermodynamics,” Phys.Rev. D13 (1976) 191–197.
[4] L. Susskind, “The world as a hologram,” J.Math.Phys. 36 (1995) 6377–6396, arXiv:hep-th/9409089 [hep-th].
[5] G. ’t Hooft, “Dimensional reduction in quantum gravity,” arXiv:gr-qc/9310026 [gr-qc].
[6] [Verlinde, 2010] Erik Verlinde. «On the Origin of Gravity and the Laws of Newton». http://arXiv:1001.0785v1 [hep-th].
[7] Margot M. Brouwer, Manus R. Visser, Andrej Dvornik, Henk Hoekstra, Konrad Kuijken, Edwin A. Valentijn, Maciej Bilicki, Chris Blake, Sarah Brough, Hugo Buddelmeijer, Thomas Erben,Catherine Heymans, Hendrik Hildebrandt, Benne W. Holwerda, Andrew M. Hopkins, Dominik Klaus, Jochen Liske, Jon Loveday, John McFarland, Reiko Nakajima, Cristóbal Sifón,Edward N. Taylor » «First test of Verlinde’s theory of Emergent Gravity using Weak Gravitational Lensing measurements»https://arxiv.org/abs/1612.03034
[8] Niayesh Afshordi, Claudio Corian, Luigi Delle Rose, Elizabeth Gould, and Kostas Skenderis » Observational Tests of Holographic Cosmology»arxiv.org/pdf/1607.04878v2.pdf
[9] George F. Smoot «Cosmic microwave background radiation anisotropies: Their discovery and utilization» REVIEWS OF MODERN PHYSICS, VOLUME 79, OCTOBER–DECEMBER 2007.
[10] V. N. Samokhvalov “Non-electromagnetic Force Interaction in Presence of Rotating Mass in Vacuum,” [International Journal of Unconventional Science] 1(1), pp. 6-19, 2013 (Article received: 18 Nov 2012; Article accepted for publication: 23 Apr 2013) http://www.unconv-science.org/en/n1/samokhvalov/